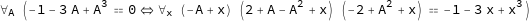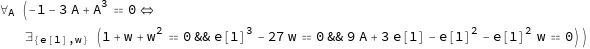位数が大きな場合
これまでの RR シリーズでは,分解体の定義多項式,primitive element による入力多項式の根の表示, primitive element を根の 線型結合で表した際の係数を古典的な Trager の方法( http://www.cecm.sfu.ca/personal/monaganm/teaching/TopicsinCA17/TragerFactor.pdf )により( http://ehito.hatenablog.com/entry/2019/02/24/150254 ),また,組成列も共役類の組み合わせ( http://ehito.hatenablog.com/entry/2019/02/13/200937 )から得ていましたが,今回は,galois 群の位数が数百程度の場合にも対応できるよう,外部ツールを用いるスタイルで再び実装しました.ただし,分解体と冪根の中間体上の定義多項式を同時に得るためにかつて用いた Groebner 基底( by asir )による方法は,次数や変数の個数の増大に敏感なため採用せず,同じく,代数体上の因数分解や GCD の利用も最小限に留めています.
具体的には
・分解体の 上の定義多項式には,pari の nfsplitting (LLL アルゴリズムによるもの)
・分解体の primitive element による入力多項式の根の表示には,同じく pari の nfisincl
・galois 群(置換表現および同型写像表現)の生成には,独自アルゴリズム(多倍長浮動小数点数によるもの)
・組成列の生成には,gap の MaximalNormalSubgroups
・円分体およびその部分体上の因数分解には,pari の nfsubfields,nffactor
・分解体の各中間体上の定義多項式には,分解体の primitive element による添加する冪根の表示(1次のみ)を用いた簡約,そのフォールバックとして Lagrange Resolvents の総和
・各中間体上の加減乗除算,GCD 計算には,maxima の algebraic モード,gcd:subres
をそれぞれ利用しています.
以下,取り敢えず,実行データを掲載します.リストの要素は
・サンプル番号
・入力多項式
・galois 群の位数
・各中間体間の拡大次数
・分解体の 上の定義多項式,primitive element による入力多項式の根の表示から,galois 群さらに組成列の生成までの時間(秒)
・分解体の各中間体上の定義多項式の生成から冪根による primitive element の表示までの時間(秒)
・上記2つの時間の合計(秒)
です.
【サンプルセット1】
サンプル番号 16 以降は,先行研究
https://core.ac.uk/download/pdf/81182361.pdf
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0920-2.pdf
http://www.jssac.org/Editor/Suushiki/V09/No1/V9N1_108.pdf
http://www.icm.tu-bs.de/ag_algebra/software/distler/Diplom.pdf (RadiRoot https://gap-packages.github.io/radiroot/ の作者の学位論文)
などからのものです.
[[1,x^2-2,[2],[2],0.708,0.002,0.71],
[2,x^3-3*x-1,[3],[3],0.552,0.139,0.691],
[3,x^4-2,[8],[2,2,2],0.37,0.006,0.376],
[4,x^4+x^2-1,[8],[2,2,2],0.509,0.006,0.515],
[5,x^4-2*x^3+2*x^2+2,[12],[3,2,2],0.842,0.134,0.976],
[6,x^4+2*x^3+3*x^2+4*x+5,[24],[2,3,2,2],0.454,0.585,1.04],
[7,x^4+x+1,[24],[2,3,2,2],0.376,0.829,1.21],
[8,x^5-2,[20],[2,2,5],1.78,0.387,2.16],
[9,x^5-5*x+12,[10],[2,5],0.455,0.302,0.757],
[10,x^5+20*x+32,[10],[2,5],0.941,0.756,1.7],
[11,x^5+11*x+44,[10],[2,5],0.161,0.404,0.565],
[12,x^5+x^4-4*x^3-3*x^2+3*x+1,[5],[5],0.277,0.178,0.455],
[13,x^5+100*x^2+1000,[20],[2,2,5],0.845,0.285,1.13],
[14,x^6+x^3+1,[6],[2,3],0.519,0.15,0.669],
[15,x^6-2,[12],[2,2,3],0.396,0.571,0.967],
[16,x^5-5*x^3+5*x-5,[20],[2,2,5],0.245,0.433,0.678],
[17,x^6+x^3+7,[18],[2,3,3],0.35,0.106,0.456],
[18,x^6-3*x^4+1,[24],[2,3,2,2],0.894,0.32,1.21],
[19,x^6+x^4-9,[24],[2,3,2,2],0.171,0.625,0.796],
[20,x^6+x^4-8,[48],[2,2,3,2,2],0.734,1.45,2.19],
[21,x^6+x^4-x^2+5*x-5,[72],[2,2,2,3,3],4.27,34.8,39.1],
[22,x^7+7*x^3+7*x^2+7*x-1,[14],[2,7],0.163,0.456,0.619],
[23,x^7-14*x^5+56*x^3-56*x+22,[21],[3,7],0.202,1.34,1.54],
[24,x^7-2,[42],[2,3,7],0.56,1.29,1.85],
[25,x^8-2*x^6-x^4+7*x^2-5*x+1,[16],[2,2,2,2],0.479,0.043,0.522],
[26,x^9+x^8+3*x^6+3*x^3-3*x^2+5*x-1,[18],[2,3,3],0.337,0.321,0.658],
[27,x^12-3,[24],[2,2,2,3],0.659,0.109,0.768],
[28,x^7-14*x^5+56*x^3-56*x+22,[21],[3,7],0.538,0.475,1.01],
[29,
x^15-x^14-14*x^13+13*x^12+78*x^11-66*x^10-220*x^9+165*x^8+330*x^7
-210*x^6-252*x^5+126*x^4+84*x^3-28*x^2-8*x+1,[15],[3,5],1.25,
0.321,1.57]]
[30,
x^14+28*x^11+28*x^10-28*x^9+140*x^8+360*x^7+147*x^6+196*x^5+336*x^4
-546*x^3-532*x^2+896*x+823,[98],[2,7,7],7.114,199.4,206.5]]
サンプル番号 30 の冪根表示.
[[c7^2*(2*e3^4-e3^2+e2^6+e2^3)+c7^3*(2*e3^4+e2^5)+c7*(e3^4-e3^2+3*e2^6+e2^3)
+c7^4*(e3^4+3*e2^6+e2^3)+e3
+c7^5*(3*e2^6-e2^5+e2^3)+e2^6+e2^5+A,A],
[e3^7+2*c7^5-c7^4+2*c7^3-c7^2+2*c7,e3],
[e2^7-4*c7^5-c7^4-3*c7^3-3*c7^2-c7-4,e2],
[c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]
【サンプルセット2】
(一部サンプルセット1と重複).一般の場合の位数は,https://mathoverflow.net/questions/143739/galois-group-of-xn-2 にあります.
[[1,x-2,[1],[],1.193,0.0,1.193],
[2,x^2-2,[2],[2],1.147,0.001,1.148],
[3,x^3-2,[6],[2,3],1.172,0.09,1.262],
[4,x^4-2,[8],[2,2,2],1.202,0.012,1.214],
[5,x^5-2,[20],[2,2,5],1.153,0.186,1.339],
[6,x^6-2,[12],[2,2,3],1.232,0.185,1.417],
[7,x^7-2,[42],[2,3,7],1.314,0.526,1.84],
[8,x^8-2,[16],[2,2,2,2],1.252,0.015,1.267],
[9,x^9-2,[54],[2,3,3,3],1.295,0.21,1.505],
[10,x^10-2,[40],[2,2,2,5],1.435,3.87,5.305],
[11,x^11-2,[110],[2,5,11],1.837,0.926,2.763],
[12,x^12-2,[48],[2,2,2,2,3],1.748,0.281,2.029],
[13,x^13-2,[156],[2,2,3,13],4.897,1.238,6.135],
[14,x^14-2,[84],[2,2,3,7],2.074,0.665,2.739],
[15,x^15-2,[120],[2,2,2,3,5],2.333,1.345,3.678],
[16,x^16-2,[64],[2,2,2,2,2,2],1.824,0.147,1.971],
[17,x^17-2,[272],[2,2,2,2,17],13.31,4.305,17.62],
[18,x^18-2,[108],[2,2,3,3,3],3.449,0.752,4.201],
[19,x^19-2,[342],[2,3,3,19],18.02,10.46,28.49],
[20,x^20-2,[160],[2,2,2,2,2,5],7.155,2.767,9.922],
[21,x^21-2,[252],[2,2,3,3,7],11.41,3.08,14.49],
[22,x^22-2,[220],[2,2,5,11],15.8,3.614,19.41],
[23,x^23-2,[506],[2,11,23],58.19,53.77,112.0],
[24,x^24-2,[96],[2,2,2,2,2,3],2.518,0.941,3.459],
[25,x^25-2,[500],[2,2,5,5,5],71.24,49.02,120.3],
[26,x^26-2,[312],[2,2,2,3,13],55.11,8.613,63.72],
[27,x^27-2,[486],[2,3,3,3,3,3],77.09,53.58,130.7],
[28,x^28-2,[336],[2,2,2,2,3,7],80.96,19.26,100.2],
[29,x^29-2,[812],[2,2,7,29],360.1,169.8,529.9],
[30,x^30-2,[240],[2,2,2,2,3,5],16.68,4.233,20.91]]
Evaluation took 352.3320 seconds (1212.0310 elapsed) using 229011.373 MB.
サンプル番号 29 の冪根表示.
[[e4+A,A],
[e4^29+89224590*c29^27+20029198*c29^26+16908450*c29^25+155757840*c29^24
+19982508*c29^23+19792500*c29^22+175147530*c29^21+19079970*c29^20
+20022702*c29^19+123821880*c29^18+11445720*c29^17+20029952*c29^16
+60090030*c29^15-20030010*c29^14+20030068*c29^13+28614300*c29^12
-83761860*c29^11+20037318*c29^10+20980050*c29^9-135087510*c29^8
+20267520*c29^7+20077512*c29^6-115697820*c29^5+23151570*c29^4
+20030822*c29^3-49164570*c29^2+40060020*c29+20030010,e4],
[c29^28+c29^27+c29^26+c29^25+c29^24+c29^23+c29^22+c29^21+c29^20+c29^19
+c29^18+c29^17+c29^16+c29^15+c29^14+c29^13+c29^12+c29^11+c29^10+c29^9
+c29^8+c29^7+c29^6+c29^5+c29^4+c29^3+c29^2+c29+1,c29]]
QE による検証
Mathematica の QE のデフォルトの議論領域は
Reduce[Exists[x, a*x^2 == 1]]
に対する出力
からも判るように複素数体であり,前回公開した Mathematica での実装の目的の 1 つは,この QE による結果の検証でした.
Mathematica で前回の各関数の定義コードを実行した後,例えば,
(p1=PL[[1]])@x
を
mp[p1];nGG[];cs[];RR[];InputForm@DP
のように処理すると
といった出力が得られます.
このとき,A についての 2 つの条件
(1) A が分解体の primitive element の定義多項式 p2 の零となる
(2) A の多項式で表された根全体 r1 /. pe -> A が入力の多項式 p1 の根全体となる
が等価であるという式
ForAll[A, Equivalent[p2@A == 0, ForAll[x, Times @@ (x - r1 /. pe -> A) == p1@x]]]
すなわち
を複素数体上で
Reduce[%,Complexes]
のように QE すると
と答えてくれます.
また,A についての 2 つの条件
(1) A が分解体の primitive element の定義多項式 p2 の零となる
(3) 出力 DP に属する全ての多項式の共通の零点 (w,e[1]) が存在する
が等価であるという式
ForAll[A, Equivalent[p2@A == 0, Exists[Evaluate@Rest@vs, And @@ (# == 0 & /@ DP)]]]
すなわち
を複素数体上で
Reduce[%,Complexes]
のように QE すると
と答えてくれます.
Mathematica 推参
オリジナルプログラムの元になったコードは Mathematica で書かれていますが,汎用性を重視した筆致なので,今回は
https://reference.wolfram.com/language/tutorial/AlgebraicNumberFields.html.ja
にある代数体関連の組み込み関数などを用いて書いてみました(取り敢えず動く程度).
なお,https://develop.open.wolframcloud.com/app/ の Create a New Notebook ボタンを押すと Mathematica がオンラインで利用できます.
(* mp *)
mp[p1_]:=Block[{c,x},
n1=Range@Exponent[p1@x,x];
r1=ToNumberField[AlgebraicNumber[Root[p1,#],{0,1}]&/@n1,All];
p2=(pe=r1[[1,1]])[[1]];(* pe is not a "AlgebraicNumber" *)
c1=Map[c,n1];
c1=c1/.SolveAlways[x==r1.c1/.pe->x,x][[1]]/.c[_]->0];
(* nGG *)
nGG[]:=Block[{x},
r12=Map[ToString,Chop[N[r1/.pe->x/.NSolve[p2@x,WorkingPrecision->50],10]],{2}];
gg=PermutationCycles/@(r12/.Thread[r12[[pe[[2]]]]->n1]);
r2=r1.Permute[c1,#]&/@gg];
(* csc and cs *)
csc[gg0_]:=Block[{},
cc=Rest@GroupOrbits[PermutationGroup@gg0,gg0];
Last@SortBy[Select[Append[#,Cycles[{}]]&/@(Union@@#&/@Subsets@cc),2*Length@#<=Length@gg0&&
GroupOrder@PermutationGroup@#==Length@#&],Length]];
cs[]:=Block[{},
cs1=NestWhileList[csc,gg,Length@#>1&];
cs2=Length/@cs1;cs3=Table[cs2[[i]]/cs2[[i+1]],{i,Length@cs2-1}]];
(* RR *)
Off[ToNumberField::nalg];
RR[]:=Block[{},
w1=ToNumberField@Exp[2*Pi*I/(ppp=LCM@@cs3)];
Print["using Cyclotomic_",ppp];
DP={Cyclotomic[ppp,w],
If[ppp==2,p2@A,First@Last@FactorList[p2@A,Extension->w1]/.p_AlgebraicNumber->ToNumberField[p,w1]/.w1[[1]]->w]};
For[i=1,i<Length@cs2,i++,LRx=Sum[w^Mod[ppp/pp*j,ppp]*Product[x-r2[[Position[gg,s][[1,1]]]],{s,PermutationProduct[PermutationPower[Complement[cs1[[i]],cs1[[i+1]]][[1]],j],#]&/@cs1[[i+1]]}],{j,pp=cs3[[i]]}];
ai=0;j=1;While[ai==0,ai=Simplify[LRx/.{w->w^j,pe->A},And@#==0&/@DP];j++];
DP=GroebnerBasis[Append[DP,Last@CoefficientList[ai,x]-e[i]],vs=Join[{A},Map[e,Reverse@Range@i],{w}]];(*Print@nputForm@DP*)]];
実行例.例によって,入力多項式の根の表示は長いので略します.
(* expamles *)
PL={#^3-3*#-1&,#^4-2&,#^4+#^2-1&,#^4-2*#^3+2*#^2+2&,#^4+2*#^3+3*#^2+4*#+5&,#^4+#+1&,#^5-2&,#^5-5*#+12&,#^5+20*#+32&,#^5+11*#+44&,#^5+#^4-4*#^3-3*#^2+3*#+1&,#^5+100*#^2+1000&,#^6+#^3+1&,#^6-2&};
(mp[#];nGG[];cs[];RR[];Print@InputForm@DP)&/@PL;//Timing
円分体の利用
RR シリーズでは冪根が代数的整数となるよう変数の導入時に係数を調整しています.これは algebraic モードへの適用を念頭に置いたものですが,1 の原始冪乗根の中間体上の定義式は必ずしも monic でないため,RR6m では,tellrat への入力の前に線形変換を施し,拡大体上の gcd 計算(それは係数に含まれる変数の線形変換と可換)の後,逆変換を施していました.
こうした局所的な往復を中間体の生成以前に 1 の原始冪乗根を導入すること,つまり,分解体の基礎体を然るべき円分体とすることで解消したのが RR7 です.
利用する円分体 Q(c_n) の n は中間体の拡大次数の最小公倍数でよいのですが,RR7 では,因数分解のコストを鑑み,各奇素因数についての円分体上での定義式の gcd を分解体の定義式としています.
今回は必要なコードを一括掲載しましたので,以下を例えば RR7.mac としてファイルに保存,load("RR7.mac")$ と読み込めば,下記の例のように実行できます.
/* examples */
PL:[x^2-2,x^3-3*x-1,x^4-2,x^4+x^2-1,x^4-2*x^3+2*x^2+2,
x^4+2*x^3+3*x^2+4*x+5,x^4+x+1,x^5-2,x^5-5*x+12,x^5+20*x+32,
x^5+11*x+44,x^5+x^4-4*x^3-3*x^2+3*x+1,x^5+100*x^2+1000,x^6+x^3+1,
x^6-2,x^5+10*x^3-10*x+4,x^5+20*x+16]$
PL3:[x^5-5*x^3+5*x+5,x^7+7*x^3+7*x^2+7*x-1,x^8-2*x^6-x^4+7*x^2-5*x+1,
x^9+x^8+3*x^6+3*x^3-3*x^2+5*x-1,x^12-3,x^7-14*x^5+56*x^3-56*x+22,
x^15-x^14-14*x^13+13*x^12+78*x^11-66*x^10-220*x^9+165*x^8+330*x^7-210*x^6-252*x^5+126*x^4+84*x^3-28*x^2-8*x+1]$
/* verbose mode on, off */
pon():=(printn(s):=print(s),printx(s):=print(s))$
poff():=(printn(s):=0,printx(s):=0)$
poff()$
/* mp */
mp(p):=block([],DEG:hipow(p,x),
[Dx,DA]:divide(p,x-A,x),t:2,K:1,KK:[1],F:[x-A],F2:[],
for i:0 unless K=0 do (
Dx:num(factor(Dx,DA)), printn("001"),
F3:[],if op(Dx)="*" then (map(lambda([s],if hipow(rat(s),x)=1 then push(s,F2) else push(s,F3)),args(Dx)),Dx:apply("*",F3),if length(F2)+length(F)=DEG then (DX:subst(A=X,DA),return(DA))),
[Dx,DB]:divide(Dx,x-B,x),push(x-B,F),
t:t+1,for j:0 while hipow(rat(gcd(f:resultant(DA,DBX:subst(B=(X-A)/(K:(-1)^t*floor(t/2)),DB),A),diff(f,X),X)),X)>0 do t:t+1, printn("002"),
push(K,KK), printn(f),
DX:factor(content(f,X)[2]), printx(DX), printn("003"),
DX:if op(num(DX))="*" then args(DX)[1] else DX,
if DEG=5 and hipow(DX,X)>20 then
(DA:0,print(concat(string(p)," is not solvable.")),return()),
printx(DX),
tellrat(DX),algebraic:on,gcd:subres,
AX:gcd(DBX,DA,A), printn("004"),
ABX:solve([AX,A+K*B-X],[A,B]),
[Dx,F,F2]:rat(subst(ABX,[Dx,F,F2])),
algebraic:off,untellrat(X),
[DA,Dx,F,F2]:subst(X=A,[DX,Dx,F,F2]),
printn(i),printx([DA,Dx,F,F2]),
if hipow(rat(Dx),x)<=1 then K:0
),
RA:sublist(flatten([F,Dx,F2]),lambda([s],not(numberp(s)))),
RA:map(lambda([s],rhs(solve(s,x)[1])),RA),
DX:subst(A=X,DA),
return(DA)
)$
/* nGG */
nGG(DA):=block([i],
er:sort(map(lambda([s],abs(s[1]-s[2])),listify(map(listify,powerset(setify(map('rhs,allroots(p))),2)))))[1]/10,
nRS:allroots(%i*DA),
GG2:nRAS:expand(map(lambda([s],subst(s,RA)),nRS)),
i:0,for s in nRAS[1] do (
i:i+1,map(lambda([t],j:1,while(j>0) do if not(integerp(t[j])) and abs(t[j]-s)<er then (t[j]:i,j:0) else j:j+1,t),GG2)),
RS:rat(map(lambda([s],KK.s),fullmapl(lambda([s],RA[s]),map(lambda([s],firstn(s,length(KK))),GG2)))),
GGRS:map("[",GG2,RS),
GG2)$
/* cs */
mul(A,B):=map(lambda([s],A[s]),B)$
inv(A):=block([B,i],B:A*(i:0),for s in A do B[s]:i:i+1,B)$
isG(GG):=is(setify(apply('append,makelist(makelist(mul(i,j),i,GG),j,GG)))=setify(GG))$
CC(GG):=block([g,C:[],G:setify(GG),H],
unless G={} do (g:listify(G)[1],
H:setify(map(lambda([s],mul(s,mul(g,inv(s)))),GG)),
G:setdifference(G,H),push(H,C)),map(listify,C))$
mnsg(GG):=block([S:0,lenGG:length(GG)],
C0:sort(CC(GG)),C01:C0[1],
PS:map(lambda([s],apply('append,listify(s))),listify(powerset(setify(rest(C0))))),
PS:map(lambda([s],append(C0[1],s)),PS), printn(length(PS)),
for d in rest(reverse(listify(divisors(lenGG)))) while S=0 do (
PS:sublist(PS,lambda([s],length(s)<=d and member(lst2:mul(lst:last(s),lst),s) and member(mul(lst2,lst),s))), printn(length(PS)),
for g in PS unless length(S:g)=d and isG(g) do S:0),S)$
cs(GG):=block([S:[GG],m:GG],unless length(m)=1 do push(m:mnsg(m),S),
csGG:[S:reverse(S),S:map(length,S),makelist(S[i-1]/S[i],i,2,length(S))])$
/* tools */
factor2list(f0):=block([f:num(f0)],if op(f)="-" then args(-f) elseif op(f)="*" then args(f) else [f])$
load("grobner")$
/* Root Of Unity */
ROU(x,N):=rat(apply("*",makelist((x^(N/s)-1)^moebius(s),s,listify(divisors(N)))))$
/* RR7 */
RR7(csGG):=block([],[cs1,cs2,cs3]:csGG,aiA:[],DAs:[],
w:if member(2,ls3:listify(setify(cs3))) then -1 else 1,
DP:map(lambda([s],Ri:rat(((ci:concat(c,s))^s-1)/(ci-1)),w:w*ci,
push(factor2list(factor(DA,Ri))[1],DAs),
[Ri,ci]),delete(2,ls3)),
printn(DP),ppp:apply("*",ls3),
map(lambda([s],tellrat(s[1])),DP),algebraic:on,
DA0:DA,map(lambda([s],DA0:gcd(DA0,s,A)),DAs),
if hipow(DA0,A)<hipow(DA,A) then
print(concat("using a factor ",string(DA0)," over the cyclotomic_",ppp)),
for i:1 thru length(cs3) do (
pp:cs3[i],map(lambda([s],tellrat(s[1])),DP),
printn("phase:"),printn([i,pp]),
/* non-zero aix and ai */
T:cs1[i+1],for g in cs1[i] while member(h:g,T) do 0,
LRx:makelist((prd:1,map(lambda([t],prd:remainder(prd*(x-assoc(t,GGRS)),DA0,A)),T:map(lambda([u],mul(h,u)),T)),prd),j,1,pp),
printn("LRx:"),printn(LRx),
ai:0,for cnt:1 while ai=0 do
(aix:sum(w^mod(ppp/pp*cnt*j,ppp)*LRx[j],j,1,pp),
ai:if aix=0 then 0 else coeff(rat(aix),x,hipow(aix,x)),
printn(concat("ai_",cnt)),printn(ai)),
if member(A,listofvars(ai)) then
(
/* def. of a[i] */
a[i]:concat(e,i),
aipp:rat(remainder(ai^pp,DA0,A)-a[i]^pp),
printn("aipp:"),printn(aipp),
/* monic rather than primitive */
a1n:num(aipp),
na1n:ifactors(abs(poly_content(coeff(a1n,a[i],0),map(second,DP)))),
na1n:apply("*",map(lambda([s],s[1]^floor(s[2]/cs3[i])),na1n)),
da1n:ifactors(abs(coeff(a1n,a[i],pp))),
da1n:apply("*",map(lambda([s],s[1]^ceiling(s[2]/cs3[i])),da1n)),
printn(na1n/da1n),
a1n:poly_normalize(subst(a[i]=na1n/da1n*a[i],a1n),[a[i]]),
tellrat(a1n),
push([a1n,a[i]],DP),
push([aiai:da1n/na1n*ai-a[i],a[i]],aiA),
/* rel-def. is gcd */
printn(LD:[last(LRx),pp,ai,a1n,aiai,DA0,DP,tellrat()]),
DA0:if hipow(aiai,A)=1 then aiai else gcd(aiai,DA0,A),
DA0:poly_normalize(DA0,[A])
),
printn([[i],DA0,DP])
),algebraic:off,map(lambda([s],untellrat(s[2])),DP),
rr5:rr3:append([[DA0,A]],DP),
for i in rest(rr3) do
if not(member(i[2],listofvars(rr4:delete(i,rr3)))) then rr3:rr4,
rr3)$
実行例.
/* オリジナルプログラム付属の例 */ for i:1 thru 15 do (print([i]),print([p:PL[i],mp(p),RR7(cs(nGG(DA)))]))$ /* 15 次,21 次拡大などの例 */ for i:1 thru 7 do (print([i]),print([p:PL3[i],mp(p),RR7(cs(nGG(DA)))]))$
それぞれの timer_info().
[[total,0.001112600037223153*sec,5373,5.978*sec,0],
[mp,0.2166666666666667*sec,15,3.25*sec,0],
[RR7,0.1295333333333333*sec,15,1.943*sec,0],
[nGG,0.03886666666666666*sec,15,0.583*sec,0],
[mul,2.706185567010309e-5*sec,3880,0.105*sec,0],
[inv,2.832415420928404e-5*sec,1271,0.036*sec,0],
[mnsg,6.216216216216216e-4*sec,37,0.023*sec,0],
[CC,5.135135135135136e-4*sec,37,0.019*sec,0],
[cs,5.333333333333334e-4*sec,15,0.008*sec,0],
[isG,1.891891891891892e-4*sec,37,0.007*sec,0],
[ROU,2.5e-4*sec,12,0.003*sec,0],
[factor2list,8.333333333333333e-5*sec,12,0.001*sec,0]]
[[total,0.003578925872983459*sec,9794,35.052*sec,0],
[mp,4.366*sec,7,30.562*sec,0],
[RR7,0.4417142857142857*sec,7,3.092*sec,0],
[nGG,0.1021428571428571*sec,7,0.715*sec,0],
[mnsg,0.0173*sec,20,0.346*sec,0],
[mul,2.711284807034685e-5*sec,8188,0.222*sec,0],
[inv,4.290657439446366e-5*sec,1445,0.062*sec,0],
[isG,4.736842105263157e-4*sec,57,0.027*sec,0],
[CC,0.00115*sec,20,0.023*sec,0],[ROU,2.5e-4*sec,8,0.002*sec,0],
[factor2list,1.25e-4*sec,8,0.001*sec,0]]
inv 再考
置換の表現には,リストタイプと巡回タイプとがあり,それぞれ積,逆元の実装に適していますが,今回のコードは根の置換という出自からリストタイプを利用しており,逆元の実装に工夫の余地がありました.現在公開中の inv は
inv(A):=map(second,sort(map("[",A,sort(A)),lambda([s,t],s[1]<t[1])))$
という sort ベースのもので
(%i3) L:random_permutation(makelist(i,i,1,10)); (%o3) [4,9,8,3,5,10,7,1,2,6] (%i5) for j:1 thru 10^5 do inv(L)$ Evaluation took 19.6490 seconds (19.6760 elapsed) using 2073.668 MB.
といった具合でした.これを積(左作用)
mul(A,B):=map(lambda([s],A[s]),B)$
と同じく成分をインデックスと見做し,第 i 成分が s である入力のリストに対して,第 s 成分が i であるリストを出力とするもの
inv(A):=block([B,i],B:A*(i:0),for s in A do B[s]:i:i+1,B)$
に変更すると
(%i7) for i:1 thru 10^5 do inv(L)$ Evaluation took 4.1150 seconds (4.1320 elapsed) using 482.180 MB.
という結果となりました.
GCD の利用
現在のオリジナルプログラムや RR6 では,分解体の primitive element A の中間体 K(w,a) 上の定義式が Lagrange resolvents の和となることを利用していますが,http://ehito.hatenablog.com/entry/2019/03/02/163023 で述べたように,A の K(w,a) 上の定義式と a の K(w) 上の定義式は,それぞれ A の K 上の定義式と冪根 a の一次の定義式との A に関する GCD と終結式(を因数分解したもの)なので,代数体での計算が高速なら,これに基づく実装の価値があります.
残念ながら maxima の因数分解は逐次代数拡大に対応していませんが,GCD は対応(algebraic モード)しており,例えば
(%i4) tellrat(a2^3+21*a1+14,a1^2+a1+1)$algebraic:on$gcd:subres$ (%i7) gcd(A^12+4*A^10+24*A^8+48*A^6-560*A^4+3136,485968*a2+A^4*(18236*a1-9524)+A^10*(83*a1-563)+655424*a1+A^8*((-739*a1)-2672)+A^6*((-2012*a1)-12700)+A^2*(474768-28560*a1)+390432,A); Evaluation took 0.0020 seconds (0.0020 elapsed) using 255.969 KB. (%o7) A^2*((12*a1+4)*a2^2+28*a2+28)-28*a2^2+((-84*a1)-28)*a2+21*A^4+392 (%i8) algebraic:off$untellrat(a1,a2)$
といった具合に,tellrat の定義式が monic(つまり,扱えるのは代数的整数のみ)という制約さえクリアすれば,...という訳で,次の RR6m を作りました(m は monic の m).
(%i15) fundef(RR6m);
(%o15) RR6m(csGG):=block([],[cs1,cs2,cs3]:csGG,kill(w),DA0:DA,Dws:[[DA,A]],DP:aiA:[],
for i thru length(cs3) do
(push([DA0,A],DP),w[i]:concat(a,2*i-1),a[i]:concat(a,2*i),
Dw:rat((w[i]^(pp:cs3[i])-1)/(w[i]-1)),Dwf:factor2list(factor(Dw,DA))[1],
if (degDwf:hipow(Dwf,w[i])) = 1
then (w[i]:rhs(solve(Dwf,w[i])[1]),
if pp > 2 then printn(concat("PROU_",pp," is a member.")))
else (push([Dwf,w[i]],Dws),push([Dwf,w[i]],DP)),tellrat(DA),algebraic:on,
T:cs1[i+1],for g0 in cs1[i] while member(g:g0,T) do 0,
LRx:makelist(apply("*",makelist(x-assoc(t,GGRS),t,T:map(lambda([u],mul(g,u)),T))),
j,1,pp),printn(LRx),algebraic:off,untellrat(A),ai:0,
for cnt while ai = 0 do
(CNT:cnt,aix:rrem(sum(w[i]^mod(cnt*j,pp)*LRx[j],j,1,pp),append(Dws,DP)),
ai:if aix = 0 then 0 else coeff(aix,x,hipow(aix,x)),printn([[cnt],ai])),
printn(Dwf),
if degDwf = 1 then w[i]:rrem(w[i],DP)
else (pop(DP),push([Dwf:poly_normalize(rrem(Dwf,DP),[w[i]]),w[i]],DP)),
printn(Dwf),printn([ai,pp,DP]),aipp:rrem(ai^pp,DP)-a[i]^pp,a1n:num(rat(aipp)),
na1n:ifactors(abs(poly_content(subst(a[i] = 0,a1n),map(second,DP)))),
na1n:apply("*",map(lambda([s],s[1]^floor(s[2]/cs3[i])),na1n)),
da1n:ifactors(abs(coeff(a1n,a[i],cs3[i]))),
da1n:apply("*",map(lambda([s],s[1]^ceiling(s[2]/cs3[i])),da1n)),
printn("na1n/da1n:"),printn(na1n/da1n),
a1n:poly_normalize(subst(a[i] = (na1n*a[i])/da1n,a1n),[a[i]]),
DP:delete([DA0,A],DP),push([a1n,a[i]],DP),push([a[i]-(da1n*ai)/na1n,a[i]],aiA),
DA0:if hipow(ai,A) = 1 then a[i]-(da1n*ai)/na1n
else (DPr:reverse(DP),sDPr:map(second,DPr),
for j thru (lDPr:length(DPr)) do
DPr:subst((vj2:sDPr[j])
= vj2
/mc[j]
:coeff(num(rat(fj1:DPr[j][1])),vj2,hipow(fj1,vj2)),
DPr),DPm:map("[",fDPr:map(first,DPr),sDPr),
[DA0m,aiaim]:subst(makelist((vj2:sDPr[j]) = vj2/mc[j],j,1,lDPr),
[DA0,a[i]-(da1n*ai)/na1n]),
print([num(rat(DA0m)),num(rat(aiaim)),A,reverse(DPm)]),
map(tellrat,fDPr),algebraic:on,
gcdA:subst(makelist((vj2:sDPr[j]) = vj2*mc[j],j,1,lDPr),
gcd(aiaim,DA0m,A)),algebraic:off,map(untellrat,sDPr),
gcdA),printn([3,DA0,DP])),rr2:[solve(DA0,A)[1],DP],
append([[DA0,A]],DP))
実行例 for i:1 thru 15 do print([p:PL[i],mp(p),RR6m(cs(nGG(DA)))]) の timer_info() では,[RR6,0.1656*sec,15,2.484*sec,0] の約 3/4 の処理時間になり,反復除算の簡約 rrem の回数も 210 から 112 になっています.
[[total,0.001120116300199891*sec,5503,6.164*sec,0],
[mp,0.2176*sec,15,3.264*sec,0],[RR6m,0.1252*sec,15,1.878*sec,0],
[nGG,0.0378*sec,15,0.5670000000000001*sec,0],
[rrem,0.002366071428571429*sec,112,0.265*sec,0],
[inv,6.372934697088908e-5*sec,1271,0.081*sec,0],
[mul,1.597938144329897e-5*sec,3880,0.062*sec,0],
[CC,6.486486486486487e-4*sec,37,0.024*sec,0],
[mnsg,4.594594594594595e-4*sec,37,0.017*sec,0],
[isG,1.351351351351351e-4*sec,37,0.005*sec,0],
[factor2list,2.702702702702703e-5*sec,37,0.001*sec,0]]
微調整
http://ehito.hatenablog.com/entry/2019/02/24/234939 の実行例の timer_info() を見ると
[[total,0.001663981382026495*sec,5586,9.295*sec,0],
[mp,0.214*sec,15,3.21*sec,0],
[nGG,0.1895333333333333*sec,15,2.843*sec,0],
[RR6,0.167*sec,15,2.505*sec,0],
[rrem,0.002457142857142857*sec,210,0.516*sec,0],
[mul,2.216494845360825e-5*sec,3880,0.08600000000000001*sec,0],
[inv,6.136900078678206e-5*sec,1271,0.078*sec,0],
[CC,8.378378378378379e-4*sec,37,0.031*sec,0],
[mnsg,4.054054054054054e-4*sec,37,0.015*sec,0],
[isG,2.162162162162163e-4*sec,37,0.008*sec,0],
[factor2list,5.405405405405407e-5*sec,37,0.002*sec,0],
[cs,6.666666666666667e-5*sec,15,0.001*sec,0]]
のように nGG が重く,その原因は例によって bfloat であろう,という訳で,書き換えてみました.
nGG(DA):=block([i],
er:sort(map(lambda([s],abs(s[1]-s[2])),listify(map(listify,powerset(setify(map('rhs,allroots(p))),2)))))[1]/10,
nRS:allroots(%i*DA),
GG2:nRAS:expand(map(lambda([s],subst(s,RA)),nRS)),
i:0,for s in nRAS[1] do (
i:i+1,map(lambda([t],j:1,while(j>0) do if not(integerp(t[j])) and abs(t[j]-s)<er then (t[j]:i,j:0) else j:j+1,t),GG2)),
RS:rat(map(lambda([s],KK.s),fullmapl(lambda([s],RA[s]),map(lambda([s],firstn(s,length(KK))),GG2)))),
GGRS:map("[",GG2,RS),
GG2)$
(なお,こうした root separation の評価は計算機代数の古典的なテーマのひとつで,例えば https://core.ac.uk/download/pdf/82808521.pdf )
結果は,...
[[total,0.001227491531467285*sec,5609,6.885*sec,0],
[mp,0.2095333333333333*sec,15,3.143*sec,0],
[RR6,0.1656*sec,15,2.484*sec,0],
[nGG,0.03653333333333333*sec,15,0.548*sec,0],
[rrem,0.002447619047619048*sec,210,0.514*sec,0],
[inv,7.002360346184106e-5*sec,1271,0.089*sec,0],
[mul,1.314432989690722e-5*sec,3880,0.051*sec,0],
[CC,8.378378378378379e-4*sec,37,0.031*sec,0],
[mnsg,4.054054054054054e-4*sec,37,0.015*sec,0],
[isG,2.432432432432433e-4*sec,37,0.009000000000000001*sec,0],
[factor2list,2.702702702702703e-5*sec,37,0.001*sec,0]]