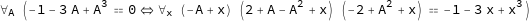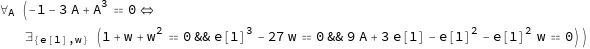2019-05-05

代数体上の多項式の高速乗算

一連の冪根拡大の構成では， $\{\sigma(A)\,|\,\sigma\in G_i\}$ を根全体とする多項式 $M_i(X,0)$ の係数 $C$ から冪根を生成し，その過程で得られる情報を $M_i(X,0)$ に還元して分解体の primitive element の最小多項式 $g_i$ を得ていますが， $C$ については $\sigma(A)$ 達の基本対称式を漸化式から得る方法，最小多項式についても幾度か述べたように例えば $g_i=\text{gcd}(g_{i-1},e_i-r_i)$ といった位置付けがあり，規模の小さな問題に対しては実用的でもある一方，こうした工夫はサイズの大きな問題に対しては実装上の問題により逆効果となります．つまり， $M_i(X,0)$ をそのまま展開することとなり，そのうちとくに負担となりえる $M_1(X,0)$ を如何に整理，展開するべきかという視点から今回の表題に至ります．

まず， $M_1(X,0)$ の計算に現れるデータのサイズがどの程度となりえるのかを例示しましょう．入力のサンプルは次の４つです．

例１　 $x^6+x^4-x^2+5 x-5$
Hirokazu Anai,Kazuhiro Yokoyama, Radical Representation of Polynomial Roots
http://www.jssac.org/Editor/Suushiki/V09/No1/V9N1_108.pdf より．
例２　 $x^{14}+28 x^{11}+28 x^{10}-28 x^9+140 x^8+360 x^7+147 x^6+196 x^5+336 x^4-546 x^3-532 x^2+896 x+823$
Andreas Distler, Ein Algorithmus zum Lösen einer Polynomgleichung durch Radikale
http://www.icm.tu-bs.de/ag_algebra/software/distler/Diplom.pdf より．
例３　 $2(1+x)^{13}-x^{13}$
例４　 $x^{13}-2$

例１，２は各先行研究において処理時間が最大，或いは結果が得られなかったもの（なお，これらは冪根拡大に限らない中間体の列を生成した後，それらの primitive element を冪根に置き換える方法によるもので，例１，２はそれぞれ逐次拡大を推奨，単純拡大を採用しています）．例４は標準的（？）なサンプルで，分解体は例３と同型ですが，生成されるデータサイズは全く異なります．

Galois 群の位数は，順に 72，98，156，156．
$\mathbb{Q}$ 上の最小分解体 $\operatorname{sp}(f)$ の $\mathbb{Q}$ 上の定義多項式の文字列としてのサイズは，順に 2208，1367，3638，159 バイト．
$\operatorname{sp}(f)$ の $\mathbb{Q}$ 上の primitive element $A$ の円分体上の最小多項式 $g_0$ の文字列としてのサイズは，順に 2208，2284，1413，132 バイト．
$\sigma(A)$ 全体の文字列としてのサイズは，順に 3276035，4452826，20461351，88263 バイト．

実際の $\sigma(A)$ の利用には
（Ａ） $\sigma(A)$ のまま用いる方法
（Ｂ） $\sigma(A)$ の $g_0$ による剰余を用いる方法
（ $f_{\mathbb{Q}}=g_0$ の場合，（Ａ），（Ｂ）は同じ）があり，展開には
（Ｃ）maxima プロパーの（乗算毎に $g_0$ による剰余をとる）方法
（Ｄ）外部ツール（Julia の Nemo パッケージ http://nemocas.org/ の ResidueRing）を呼び出す方法
があります．各場合の入力から出力までの時間は，次の通りです．

（Ａ），（Ｃ）の場合，順に 23.89，127.47，643.56，7.15 秒．
（Ａ），（Ｄ）の場合，順に 19.88，50.35，175.85，7.43 秒．
（Ｂ），（Ｃ）の場合，順に 24.05，86.62，128.49，3.82 秒．
（Ｂ），（Ｄ）の場合，順に 19.80，50.75，229.23，3.86 秒．

なお，上記の Nemo の ResidueRing は同パッケージの NumberField や Hecke パッケージ http://thofma.github.io/Hecke.jl/latest/ の代数体関連の関数よりも高速です．また，giac https://www-fourier.ujf-grenoble.fr/~parisse/giac.html で乗算毎に rem を用いる方法では

（Ｂ），（Ｄ）の場合，順に 21.83，51.03，397.46，3.94 秒

となります．

2019-04-19

改善策と問題点

前々回の記事（ http://ehito.hatenablog.com/entry/2019/04/11/193241 ）で述べた方法では， $M_i(X,1)$ 以降をただ $1$ つの $r_i$ を見付けるために生成していますが，実は $M_i(X,0)$ を得た段階で，それが $F_{i-1}[X]$ に属する場合には，先述の通り拡大を行わず，属さない場合，つまり， $M_i(X,0)$ が $C\in F_{i}\setminus F_{i-1}$ となる係数 $C$ をもつ場合には，その Lagrange Resolvent

$\begin{align} R_i(k)&=\sum_{j=0}^{p_i-1} \zeta^{j k P/p_i} \tau^j(C)\ \ (k=1,\ldots,p_i-1) \end{align}$

の中に $0$ でないものがあるので，それを $r_i$ とすることができます．

この方法では，全ての係数を生成するのは $g_i$ に直結した $M_i(X,0)$ のみで，後は $1$ つの係数 $C$ に対する処理となり，相応の高速化が期待できるように思えます．

ところが，この $\tau^j(C)\ (j=1,\ldots,p_i-1)$ を定義通りに計算すると， $C$ は $\sigma(A)\, (\sigma\in G_i)$ の基本対称式の $1$ つゆえ， $C=S(A)$ となる $F_{i-1}$ 上の多項式 $S$ があり， $\tau$ の準同型性から， $\tau^j(S(A))=S(\tau^j(A))$ なので， $\tau^j$ に対応する $f_{\mathbb{Q}}$ の根を $S(A)$ の $A$ に代入したもの，つまり，最も悪い場合には， $f_{\mathbb{Q}}$ の次数のおよそ $2$ 乗の次数の多項式（しかも係数は分子分母の桁数が大変なことになっている既約分数）の簡約整理が必要となります．

これまでのところ
【１】前々回の記事のままの実装
【２】上記の改善策による実装
そして
【３】上記の $C$ に対する次数よりも大きな次数の項を消去しながら $R_i(X,k)$ を簡約整理する実装
の処理時間は，サイズの小さな問題では【２】が短く，大きな問題では【１】が短く，【３】はその中間といった実験結果を得ています．

2019-04-13

A comparison of splitting field calculators

方程式 f=0 の Gaolis 群の元の陽な表示（置換や同型写像）の取得には「分解体の定義多項式」と「 primitive element による f の根の多項式表示」の利用が古典的です．そこで今回は，幾つかの計算機代数システムについて，当該処理を担当する関数によるサンプルの処理時間を比較します．

比較する関数は
・mp9 on maxima（Trager の方法による自作関数です）
・splitfield on maxima（Trager の方法による組み込み関数ですが，現在のマニュアルには載っていません）
・SplittingField，FactorsPolynomialAlgExt on GAP（それぞれ Radiroot，Alnuth パッケージの関数です）
・SplittingField on Magma（online の Magma Calculator での実行です）
・nfsplitting，nfisincl on PARI（本命です）
・sp on Asir（逐次拡大は魅力的ですが，．．．）

入力サンプルは，セットＡが以下のもの，セットＢが x^i-2 (i=2,3,...) です．

      [[1,x^2-2],[2,x^3-3*x-1],[3,x^4-2],[4,x^4+x^2-1],[5,x^4-2*x^3+2*x^2+2],
       [6,x^4+2*x^3+3*x^2+4*x+5],[7,x^4+x+1],[8,x^5-2],[9,x^5-5*x+12],
       [10,x^5+20*x+32],[11,x^5+11*x+44],[12,x^5+x^4-4*x^3-3*x^2+3*x+1],
       [13,x^5+100*x^2+1000],[14,x^6+x^3+1],[15,x^6-2],[16,x^5-5*x^3+5*x-5],
       [17,x^6+x^3+7],[18,x^6-3*x^4+1],[19,x^6+x^4-9],[20,x^6+x^4-8],
       [21,x^6+x^4-x^2+5*x-5],[22,x^7+7*x^3+7*x^2+7*x-1],
       [23,x^7-14*x^5+56*x^3-56*x+22],[24,x^7-2],
       [25,x^8-2*x^6-x^4+7*x^2-5*x+1],[26,x^9+x^8+3*x^6+3*x^3-3*x^2+5*x-1],
       [27,x^12-3],[28,x^7-14*x^5+56*x^3-56*x+22],
       [29,
        x^15-x^14-14*x^13+13*x^12+78*x^11-66*x^10-220*x^9+165*x^8+330*x^7
            -210*x^6-252*x^5+126*x^4+84*x^3-28*x^2-8*x+1]]

実験結果です．

・mp9 on maxima
セットＡ（21 で挫折）　Evaluation took 99.2830 seconds (107.5700 elapsed) using 7036.517 MB.
セットＢ（i=7 で挫折）　Evaluation took 0.0900 seconds (0.4580 elapsed) using 9.523 MB.

・splitfield on maxima
セットＡ（21 で挫折）　Evaluation took 121.7320 seconds (126.9250 elapsed) using 9229.759 MB.
セットＢ（i=7 で挫折）　Evaluation took 0.1750 seconds (0.1760 elapsed) using 57.411 MB.

・SplittingField，FactorsPolynomialAlgExt on GAP
セットＡ
x:=Indeterminate(Rationals,"x");P:=[x^2-2,...];
Rt0:=Runtimes();for i in [1..29] do
p:=P[i];sp:=SplittingField(p);FactorsPolynomialAlgExt(sp,p); od;
Rt:=Runtimes();Rt.user_time-Rt0.user_time;
17.215 seconds.
セットＢ（i=13 で挫折）
x:=Indeterminate(Rationals,"x");
Rt0:=Runtimes();for i in [1..12] do
p:=x^i-2;sp:=SplittingField(p);FactorsPolynomialAlgExt(sp,p); od;
Rt:=Runtimes();Rt.user_time-Rt0.user_time;
21.110 seconds.

・SplittingField on Magma
セットＡ　
R:=PolynomialRing(IntegerRing());P:=[x^2-2,...];
for i:=1 to 29 do sp:=SplittingField(P[i]); end for;
Total time: 3.020 seconds.
セットＢ（i=19で挫折）
R:=PolynomialRing(IntegerRing());
for i:=2 to 18 do sp:=SplittingField(x^i-2); end for;
Total time: 57.450 seconds.

・nfsplitting，nfisincl on PARI
セットＡ
P=[x^2-2,...];
for(i=1,29,p=P[i];sp=nfsplitting(p);nfisincl(p,subst(sp,x,a)));
time = 772 ms.
セットＢ　
for(i=1,18,p=x^i-2;sp=nfsplitting(p);nfisincl(p,subst(sp,x,a)));
time = 13,509 ms.
for(i=19,30,p=x^i-2;sp=nfsplitting(p);nfisincl(p,subst(sp,x,a)));
time = 10min, 56,209 ms.

・sp on Asir
セットＡ
load("sp")$P=[x^2-2,...]$T=time()[0]$N=0$while(N<29){print([N]);sp(P[N]);N++;}$time()[0]-T;
2.29462 seconds.
セットＢ（i=20で挫折）
T=time()[0]$N=2$while(N<=19){print([N]);sp(x^N-2);N++;}$time()[0]-T;
4462.29 seconds.

2019-04-11

冪根拡大の新たな構成法

$\mathbb{Q}$ 上の既約多項式 $f$ に対して，次が既知であるとします．
（１） $f$ の $\mathbb{Q}$ 上の最小分解体 $\operatorname{sp}(f)$ の定義多項式 $f_\mathbb{Q}$ （つまり， $\operatorname{sp}(f)$ の primitive element $\alpha$ の $\mathbb{Q}$ 上の最小多項式）
（２） $f$ の各根 $\in\mathbb{Q}[A]$ （ $A$ は $\alpha$ に対応する変数）
（３）各 $\sigma\in\operatorname{Gal}(\operatorname{sp}(f)/\mathbb{Q})$ についての $\sigma(A)$ （つまり， $f_\mathbb{Q}$ の根 $\in\mathbb{Q}[A]$ ）および $f$ の根の列に対する置換としての $\sigma$ の表示
（４）組成列 $\operatorname{Gal}(\operatorname{sp}(f)/\mathbb{Q})=G_0\supset G_1\supset\ldots\supset G_n=\{\operatorname{id}\}$
そして， $p_i=|G_{i-1}|/|G_i|\,(i=1,\ldots,n)$ の全てが素数であるとします．

このとき，然るべき円分体 $F_0$ に幾つかの冪根 $r_1,\ldots,r_m$ を逐次添加して，拡大体の列 $\mathbb{Q}\subset F_0\subset F_1 \subset\ldots\subset F_m\,\left(\supset\operatorname{sp}(f)\right)$ を構成する，すなわち，
（５） $F_0$
および，各 $i\in\{1,\ldots,m\}$ について
（６） $F_i=F_{i-1}(r_i)$ の $F_{i-1}$ 上の定義多項式 $f_i$ （つまり， $r_i$ の $F_{i-1}$ 上の最小多項式）
そして，各 $i\in\{0,\ldots,m\}$ について
（７） $\alpha$ の $F_i$ 上の最小多項式 $g_i$
を得る新たな方法を案出しましたので，その概要を述べます．

まず，各 $p\in\{p_1,\ldots,p_n\}\setminus\{2\}$ に対する $1$ の原始 $p$ 乗根の $1$ つ $\zeta_p$ を $\mathbb{Q}$ に添加した体を $F_0$ と定め， $f_{\mathbb{Q}}$ の各 $p$ 分体上の既約因数を $1$ つずつ取り出し，それらの $F_0$ 上での GCD を $g_0$ とする（各 $p$ 分体上での因数分解は，その適当な部分体上での分解を挟むと処理時間が短縮できる場合がある）．

次に， $\{p_1,\ldots,p_n\},\ \{\zeta_{p_1},\ldots,\zeta_{p_n}\}$ の要素の総積をそれぞれ $P,\ \zeta$ とおくと，各 $i\in\{1,\ldots,n\}$ に対して， $\zeta^{P/p_i}$ は $1$ の原始 $p_i$ 乗根となり， $\tau\in G_{i-1}\setminus G_i$ を固定して

$\begin{align} M_i(X,j)&=\prod_{\sigma\in \tau^j G_i} (X-\sigma(A))\ \ (j=0,\ldots,p_i-1),\\ R_i(X,k)&=\sum_{j=0}^{p_i-1} \zeta^{j k P/p_i} M_i(X,j)\ \ (k=1,\ldots,p_i-1) \end{align}$

とおく．この右辺の計算は， $g_{i-1},f_{i-1},\ldots,f_1$ （ $i=1$ のときは $g_0$ のみ）および円分多項式 $\Phi_p\ (p\in\{p_1,\ldots,p_n\}\setminus\{2\})$ による簡約を挟んで行い，

・ $M_i(X,0)\in F_{i-1}[X]$ の場合，そこで処理を止め， $F_i=F_{i-1},\ g_i=g_{i-1}$ と定めて，体の拡大は行わない（ $f_i$ は定義しない）．

・そうでない場合， $R_i(X,k)$ が零多項式にならない $k$ があり，その零でない係数の $1$ つを $r_i$ とすると， ${r_i}^j\ (j=1,\ldots,p_i-1)$ には $A$ が含まれ， ${r_i}^{p_i}\in F_{i-1}$ となるので， $F_i=F_{i-1}(r_i),\ f_i(e_i)={e_i}^{p_i}-{r_i}^{p_i}$ （ $e_i$ は $r_i$ に対応する変数だが， $r_i$ の適当な有理数倍に対応させて余分な冪乗を含まない整数係数の monic な $f_i$ を得ることもできる）と定める．また，

${e_i}^j-{r_i}^j=0\ \ (j=1,\ldots,p_i-1)$

を $A^s\ (s=1,\ldots)$ についての連立 $1$ 次方程式として解いたものを

$\displaystyle M_i(X,0)=\prod_{\sigma\in G_i} (X-\sigma(A))$

を簡約したものに含まれる各 $A^s\ (s=1,\ldots)$ に代入して得られる多項式（この連立 $1$ 次方程式の解は一般に一意的ではないが代入すれば打ち消し合う．結果の多項式は Groebner 基底や終結式から得ることもできる）を monic にしたものを $g_i$ と定める．

以上で拡大しなかった体を取り除き，添え字を詰める．

上記の方法は（７）の算出において，冪根 $r_i$ の $p_i-1$ までの冪から得られる $F_i$ 上の連立 $1$ 次方程式を用いて $A^s$ を直接消去する点が特徴で，全ての $k$ に亘る Resolvent の和を取る方法があくまで多項式としての扱いを要請するのに対して，上記の $R_i(X,k)$ は多くの場合に $R_i(1,k)$ といったもの（つまり， $\sigma(A)\ (\sigma\in G_i)$ の基本対称式の線形結合）で代替できます．

例１　 $f=x^3-3x-1$ の場合
（１） $f_{\mathbb{Q}}=A^3-3A-1$
（３） $[ [[1,2,3],A], [[2,3,1],2-A^2], [[3,1,2],A^2-A-2]]$
（４） $G_0\cong\{[1,2,3],[2,3,1],[3,1,2]\}$ ， $G_1\cong\{[1,2,3]\}$
（５） $F_0=\mathbb{Q}(\zeta_3)$ ， $\Phi_3=c_3^2+c_3+1$ （ $c_p$ は $\zeta_p$ に対応する変数）， $g_0=A^3-3A-1$
となり， $\tau(A)=2-A^2$ とすれば $M_1(X,0)=X-A,\ M_1(X,1)=X+A^2-2,\ M_1(X,2)=X-A^2+A+2$ ，従って， $R_1(X,1)=(2c_3+1)A^2-(c_3+2)A-4c_3-2$ なので，これ自体を $r_1$ として $F_1=F_0(r_1),\ 3 e_1=r_1$ とおけば， $F_0$ 上では ${r_1}^3=27c_3$ により， $f_1(e_1)=e_1^3-c_3$ となり， $3e_1={r_1},\ (3e_1)^2={r_1}^2$ に対して $A_s=A^s\ (s=1,2)$ とおいて得られる $(-3 e_1)+A_2 (2c_3+1)-4c_3+A_1((-c_3)-2)-2=0,\ (-3e_1^2)+A_2(c_3+2)-2c_3+A_1((-2c_3)-1)-4=0$ を $F_1$ 上で解いた $A_1 = (c_3+1)e_1^2-e_1,\ A_2 = e_1^2+((-c_3)-1)e_1+2$ を $X-A_1$ に代入，変数 $X$ を $A$ に改めれば $(-c_3e_1^2)-e_1^2+e_1+A$ となり， $[[(-c_3 e_1^2)-e_1^2+e_1+A,A],[e_1^3-c_3,e_1],[c_3^2+c_3+1,c_3]]$ に至ります．

例２　実際には，連立方程式を解くことなく， $A$ を主変数として $e_i-r_i$ による剰余をとるだけで $M_i(X,0)$ から $A$ を消去できる場合が多く，以下，その場合には rem，連立方程式を解いた場合には ls を拡大次数 $p_i$ と合わせて表示した実行例を掲載します．タイミングデータは，いずれも（１）から（７）までの算出時間の合計です．

[1] 
[2,rem] 
[x^2-2,[[e1+A,A],[e1^2-2,e1]]] 
[2] 
[3,ls] 
[x^3-3*x-1,[[(-c3*e1^2)-e1^2+e1+A,A],[e1^3-c3,e1],[c3^2+c3+1,c3]]] 
[3] 
[2,rem] 
[2,rem] 
[2,rem] 
[x^4-2,[[2*e3+e2+A,A],[e3^2+e1,e3],[e2^2-e1,e2],[e1^2-2,e1]]] 
[4] 
[2,rem] 
[2,rem] 
[2,rem] 
[x^4+x^2-1,[[(2*e3+e2)/2+A,A],[e3^2+2*e1+2,e3],[e2^2-2*e1+2,e2],[e1^2-5,e1]]] 
[5] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^4-2*x^3+2*x^2+2,
 [[e3/21+A,A],[e3^2+42*e2+126*c3*e1^2+42*e1^2+294*e1+294,e3],
  [e2^2-210*e1^2+c3*((-42*e1^2)-588*e1)-294*e1+1323,e2],[e1^3+21*c3+14,e1],
  [c3^2+c3+1,c3]]]
  
[6] 
[2,rem] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^4+2*x^3+3*x^2+4*x+5,
 [[(2*e4+e3-585)/585+A,A],
  [e4^2+c3*((-690*e1*e2^2)+315*e2^2+8775*e2)-30*e1*e2^2+675*e2^2+35100*e2
       +342225,e4],
  [e3^2+c3*(660*e1*e2^2+360*e2^2-35100*e2)+690*e1*e2^2-315*e2^2-26325*e2
       +342225,e3],[e2^3-8010*e1+c3*(4860-6300*e1)-2295,e2],[e1^2-3,e1],
  [c3^2+c3+1,c3]]]
  
[7] 
[2,rem] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^4+x+1,
 [[(2*e4+e3)/624+A,A],
  [e4^2+c3*((-46*e1*e2^2)-126*e2^2+4992*e2)-2*e1*e2^2-270*e2^2+19968*e2,e4],
  [e3^2+c3*(44*e1*e2^2-144*e2^2-19968*e2)+46*e1*e2^2+126*e2^2-14976*e2,e3],
  [e2^3-1068*e1+c3*((-840*e1)-3888)+1836,e2],[e1^2-229,e1],[c3^2+c3+1,c3]]]
  
[8] 
using a factor (-30*c5^3)+10*c5^2-20*c5+A^5-10 over the cyclotomic_5 
[5,rem] 
[x^5-2,[[e3+A,A],[e3^5+30*c5^3-10*c5^2+20*c5+10,e3],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[9] 
[2,rem] 
[5,ls] 
[x^5-5*x+12,
 [[(c5^2*(e1*(21*e2^4+55*e2^3+75*e2^2)-90*e2^4+125*e2^3-250*e2^2)
    +c5^3*(e1*(21*e2^4+15*e2^3+75*e2^2)-20*e2^4+125*e2^3)-55*e2^4
    +e1*((-12*e2^4)+35*e2^3-25*e2^2)+c5*((-110*e2^4)+70*e1*e2^3-250*e2^2)
    -75*e2^3-125*e2^2+625*e2)
    /3125
    +A,A],
  [e2^5-1875*e1+c5^3*(3125-3750*e1)+c5^2*((-3750*e1)-9375)-6250*c5-3125,e2],
  [e1^2+10,e1],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[10] 
[2,rem] 
[5,ls] 
[x^5+20*x+32,
 [[A-(c5^2*(e1*(8*e2^4+40*e2^3+200*e2^2)+20*e2^4-50*e2^3+500*e2^2)
     +c5^3*(e1*(8*e2^4+20*e2^3+200*e2^2)+10*e2^4-50*e2^3)
     +c5*(30*e2^4+60*e1*e2^3+500*e2^2)+15*e2^4+e1*((-e2^4)+30*e2^3-150*e2^2)
     +250*e2^2-2500*e2)
     /12500,A],
  [e2^5+c5^2*(32500*e1+12500)+c5^3*(32500*e1-87500)+47500*e1-75000*c5-37500,
   e2],[e1^2+5,e1],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[11] 
[2,rem] 
[5,ls] 
[x^5+11*x+44,
 [[A-(c5^2*(e1*(189*e2^4+1045*e2^3+4235*e2^2)+350*e2^4-935*e2^3+6050*e2^2)
     +c5^3*(e1*(189*e2^4+385*e2^3+4235*e2^2)+100*e2^4-935*e2^3)
     +c5*(450*e2^4+1430*e1*e2^3+6050*e2^2)+225*e2^4
     +e1*((-83*e2^4)+715*e2^3-2420*e2^2)+385*e2^3+3025*e2^2-33275*e2)
     /166375,A],
  [e2^5+c5^2*(35475*e1-6875)+c5^3*(35475*e1-34375)+41800*e1-41250*c5-20625,
   e2],[e1^2+2,e1],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[12] 
[5,ls] 
[x^5+x^4-4*x^3-3*x^2+3*x+1,
 [[(c5^3*(10*e1^4-22*e1^3-363*e1^2)+16*e1^4+c5^2*((-10*e1^4)-99*e1^3-121*e1^2)
                                   +c5*((-25*e1^4)-66*e1^3+121*e1^2)-132*e1^3
                                   -121*e1^2+1331*e1+1331)
    /6655
    +A,A],[e1^5-165*c5^3-385*c5^2-275*c5-451,e1],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[13] 
using a factor 5000*c5^3+A^3*((-40*c5^3)-40*c5^2-20)+A^2*((-300*c5^3)+100*c5^2-200*c5-100)+7000*c5^2+12000*c5+A^5+1000*A+6000 over the cyclotomic_5
  
[5,ls] 
[x^5+100*x^2+1000,
 [[((-e3^4)+c5^2*((-2*e3^4)+6*e3^3-8*e3^2)+c5*((-2*e3^4)-12*e3^2)
           +c5^3*(6*e3^3-4*e3^2)-2*e3^3-6*e3^2+20*e3)
    /20
    +A,A],[e3^5+240*c5^3-80*c5^2+160*c5+80,e3],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[14] 
using a factor A^3-c3 over the cyclotomic_3 
[3,rem] 
[x^6+x^3+1,[[e2+A,A],[e2^3+c3,e2],[c3^2+c3+1,c3]]] 
[15] 
using a factor (-720*c3)+A^6-74 over the cyclotomic_3 
[2,rem] 
[3,rem] 
[x^6-2,[[e3+A,A],[e3^3-18*c3*e1-19*e1,e3],[e1^2-2,e1],[c3^2+c3+1,c3]]] 
[16] 
using a factor A^2*(1875*c5^3+1875*c5^2+3125)+A^6*(175*c5^3+175*c5^2+350)+5775*c5^3+A^8*((-10*c5^3)-10*c5^2-30)+A^4*((-1000*c5^3)-1000*c5^2-1750)+5775*c5^2+A^10+9450 over the cyclotomic_5
  
[2,rem] 
[5,ls] 
[x^5-5*x^3+5*x-5,
 [[A-(c5^2*(3*e2*e3^4-10*e3^4)+3*c5^3*e2*e3^4-2*e2*e3^4-10*c5*e3^4-5*e3^4
                              -80*e3)
     /160,A],[e3^5-80*e2-1200*c5^3+400*c5^2-800*c5-400,e3],
  [e2^2+231*c5^3+231*c5^2+378,e2],[c5^4+c5^3+c5^2+c5+1,c5]]]
  
[17] 
using a factor 162*c3+A^6*((-18*c3)-9)+A^9+108*A^3+81 over the cyclotomic_3 
[3,ls] 
[3,rem] 
[x^6+x^3+7,
 [[(7*e3+3*c3*e2^2+e2^2)/7+A,A],[e3^3+3*c3+1,e3],[e2^3-3*c3+5,e2],
  [c3^2+c3+1,c3]]]
  
[18] 
[2,rem] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^6-3*x^4+1,
 [[e4+e3+A,A],
  [e4^2+c3*(4*e1*e2^2*e3-3*e2^2+e2)+e1*(4*e2^2*e3-4*e2*e3)-4*e2^2+4*e2-5,e4],
  [e3^2+e2^2-c3*e2-e2-1,e3],[e2^3-c3,e2],[e1^2+1,e1],[c3^2+c3+1,c3]]]
  
[19] 
[2,rem] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^6+x^4-9,
 [[e4/156+A,A],
  [e4^2+1872*e3+c3*((-3780*e1*e2^2)-52056*e2^2)+1026*e1*e2^2-76638*e2^2
       +4056*e2+40560,e4],
  [e3^2+c3*(e1*(2*e2^2-260*e2)+810*e2^2+4212*e2)+432*e2^2
       +e1*((-44*e2^2)-364*e2)-1404*e2,e3],
  [e2^3-3204*e1+c3*((-2520*e1)-34704)+16388,e2],[e1^2+239,e1],[c3^2+c3+1,c3]]]
  
[20] 
[2,rem] 
[2,rem] 
[3,ls] 
[2,rem] 
[2,rem] 
[x^6+x^4-8,
 [[(e5+14*e4)/1029+A,A],
  [e5^2+c3*(e1*(e2*(294*e3*e4-282*e3^2*e4)+583884*e3^2)
           +e2*(864*e3^2*e4+21168*e3*e4)+4655784*e3^2-230496*e3)
       +e1*(e2*(1911*e3*e4-69*e3^2*e4)+683550*e3^2)
       +e2*(2970*e3^2*e4+7938*e3*e4)-2878407*e3^2+266511*e3+3529470,e5],
  [e4^2+c3*((-1692*e1*e3^2)+5136*e3^2+1176*e3)-414*e1*e3^2+17655*e3^2+441*e3
       +7203,e4],[e3^3+c3*(1716*e1+38520)-2382*e1+34561,e3],[e2^2-2,e2],
  [e1^2+106,e1],[c3^2+c3+1,c3]]]
  
[21] 
<permutation group with 72 generators>
[2,rem] 
[2,rem] 
[2,rem] 
[3,ls] 
[3,ls] 
[x^6+x^4-x^2+5*x-5,
 [[A-(c3*(e1*(20*e3*e5^2-486*e5^2-7938*e4^2)-60*e3*e5^2+810*e5^2-13230*e4^2)
     +e1*(37*e3*e5^2+27*e5^2-441*e2*e4^2-3969*e4^2)-111*e3*e5^2-45*e5^2
     -1176*e5-1323*e2*e4^2-6615*e4^2-3528*e4)
     /7056,A],[e5^3+c3*(240*e3+1944*e1)-204*e3+2052*e1,e5],
  [e4^3-4*e2+24*c3*e1+12*e1,e4],[e3^2+4*e1+143,e3],[e2^2-4*e1+143,e2],
  [e1^2-5,e1],[c3^2+c3+1,c3]]]
  
[22] 
using a factor 42*c7^4+A^2*((-14*c7^4)-14*c7^2-14*c7-7)+42*c7^2+42*c7+A^7-7*A^5+49*A+21 over the cyclotomic_7
  
[7,ls] 
[x^7+7*x^3+7*x^2+7*x-1,
 [[(c7^4*(25*e2^6+56*e2^5-490*e2^4+686*e2^3-2401*e2^2)
    +c7*(24*e2^6-490*e2^4-4802*e2^2)+c7^5*(16*e2^6-28*e2^5-343*e2^4-4802*e2^2)
    +c7^2*(8*e2^6-28*e2^5-147*e2^4)+12*e2^6
    +c7^3*((-e2^6)+56*e2^5+686*e2^3-2401*e2^2)+91*e2^5-245*e2^4+1029*e2^3
    -2401*e2^2+16807*e2)
    /117649
    +A,A],
  [e2^7+84035*c7^5-184877*c7^4-689087*c7^3-957999*c7^2-873964*c7-436982,e2],
  [c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]]
  
[23] 
using a factor A*(392*c7^5+1176*c7^4+1176*c7^3+392*c7^2-784)+84*c7^5+A^3*((-56*c7^5)-280*c7^4-280*c7^3-56*c7^2+280)+A^5*(14*c7^4+14*c7^3-28)+224*c7^4+224*c7^3+84*c7^2+A^7-126 over the cyclotomic_21
  
[7,ls] 
[x^7-14*x^5+56*x^3-56*x+22,
 [[A-(37*c7^5*e2^6+34*c7^4*e2^6+c7^3*e2^6+15*c7^2*e2^6+44*c7*e2^6+16*e2^6
                  -224*e2)
     /224,A],[e2^7-196*c7^5+42*c7^4+196*c7^3+574*c7^2+462*c7+294,e2],
  [c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]]
  
[24] 
using a factor (-84*c7^5)-112*c7^4-28*c7^3-56*c7^2-140*c7+A^7-70 over the cyclotomic_21
  
[7,rem] 
[x^7-2,
 [[e3+A,A],[e3^7+84*c7^5+112*c7^4+28*c7^3+56*c7^2+140*c7+70,e3],
  [c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]]
  
[25] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[x^8-2*x^6-x^4+7*x^2-5*x+1,
 [[(e4+e3+2*e2+4*e1)/8+A,A],[e4^2+e1*(6*e2+8)-2*e2-32,e4],
  [e3^2+e1*(2*e2-8)-14*e2-32,e3],[e2^2+2*e1+10,e2],[e1^2-5,e1]]]
  
[26] 
[2,rem] 
[3,ls] 
[3,ls] 
[x^9+x^8+3*x^6+3*x^3-3*x^2+5*x-1,
 [[(c3*(e2^2*(680352*e3^2+180787068)+808082*e1*e2*e3^2+202593204*e3^2)
    +e1*(404041*e2*e3^2-12575046*e3^2+e2^2*((-40541*e3^2)-116220258))
    +e2*(9707841*e3^2+18750201624)+e2^2*(340176*e3^2+90393534)+101296602*e3^2
    +1704563784*e3)
    /337503629232
    +A,A],
  [e3^3-35079*e2^2+e1*((-6237*e2^2)+32670*e2-574992)
       +c3*((-70158*e2^2)+65340*e1*e2-13224816)-498762*e2-6612408,e3],
  [e2^3+108*e1+168*c3+84,e2],[e1^2+199,e1],[c3^2+c3+1,c3]]]
  
[27] 
using a factor A^6*((-104*c3)-52)+A^12-3 over the cyclotomic_3 
[2,rem] 
[2,rem] 
[3,rem] 
[x^12-3,
 [[e4/6+A,A],[e4^3-72*c3*e1*e2-36*e1*e2-108*e2,e4],[e2^2-52*e1-90,e2],
  [e1^2-3,e1],[c3^2+c3+1,c3]]]
  
[28] 
using a factor A*(392*c7^5+1176*c7^4+1176*c7^3+392*c7^2-784)+84*c7^5+A^3*((-56*c7^5)-280*c7^4-280*c7^3-56*c7^2+280)+A^5*(14*c7^4+14*c7^3-28)+224*c7^4+224*c7^3+84*c7^2+A^7-126 over the cyclotomic_21
  
[7,ls] 
[x^7-14*x^5+56*x^3-56*x+22,
 [[A-(37*c7^5*e2^6+34*c7^4*e2^6+c7^3*e2^6+15*c7^2*e2^6+44*c7*e2^6+16*e2^6
                  -224*e2)
     /224,A],[e2^7-196*c7^5+42*c7^4+196*c7^3+574*c7^2+462*c7+294,e2],
  [c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]]
  
[29] 
[3,ls] 
[5,ls] 
[x^15-x^14-14*x^13+13*x^12+78*x^11-66*x^10-220*x^9+165*x^8+330*x^7-210*x^6
     -252*x^5+126*x^4+84*x^3-28*x^2-8*x+1,
 [[(c5^2*(c3*(e1*(525953392818*e2^4+46208521901700*e2^3+5483213506110420*e2^2)
             +e1^2*((-62302134318*e2^4)-29074162205952*e2^3
                                       -610836365423592*e2^2))
         +e1*(116400133372*e2^4-111709403146002*e2^3+1413356700403458*e2^2)
         +e1^2*(35740453538*e2^4-16527048188010*e2^3+404838613165410*e2^2)
         +2554940802905*e2^4+5884406978016*e2^3+298462719049948368*e2^2)
    +c5*(c3*(e1^2*(79051166520*e2^4+13259732939685*e2^3+1650568846264596*e2^2)
            +e1*((-13970179140*e2^4)-61606115074863*e2^3
                                    +8506698305265252*e2^2))
        +e1*(396789211070*e2^4+17170190959320*e2^3+15616854293421456*e2^2)
        +e1^2*(63547608910*e2^4+782091603927*e2^3+2793257089431372*e2^2)
        -1132510352465*e2^4-694234588400388*e2^3+121491722900512989*e2^2)
    +c5^3*(c3*(e1^2*(60994007362*e2^4+9958452196578*e2^3
                                     -1843804912740354*e2^2)
              +e1*((-8979432782*e2^4)-26288677701354*e2^3
                                     +1084484608686126*e2^2))
          +e1*(307652844052*e2^4+29544771597858*e2^3-8622588208586724*e2^2)
          +e1^2*(49331767338*e2^4+3917263880256*e2^3-1355756659169274*e2^2)
          -2420808895895*e2^4-1081854379975083*e2^3+173521417632078870*e2^2)
    +c3*(e1*(338714791972*e2^4+103803801230007*e2^3+5905815006243258*e2^2)
        +e1^2*((-8749508036*e2^4)-8422621998885*e2^3-5198921087024934*e2^2
                                 +359767749025048144986))
    +e1*(237056535124*e2^4+42986287364100*e2^3-21939579777759444*e2^2
                          +1858800036629415415761)
    +e1^2*(49161208632*e2^4+10281781872597*e2^3-3348131738146902*e2^2
                           +299806457520873454155)-116094621149*e2^4
    -95925022751778*e2^3+270729765065001618*e2^2+59961291504174690831*e2
    -1858800036629415415761)
    /27882000549441231236415
    +A,A],
  [e2^5+c5*(6358442085*e1^2+c3*(313059766185*e1-54981822735*e1^2)
                           -23189612310*e1-2516072935635)-101660268159*e1^2
       +c5^2*((-13838962185*e1^2)+c3*(150732480015*e1-46753250625*e1^2)
                                 -115948061550*e1-2156633944830)
       +c3*((-103904424189*e1^2)-90439488009*e1)
       +c5^3*((-116696113560*e1^2)+c3*((-89018189190*e1^2)-255085735410*e1)
                                  -672498756990*e1-3594389908050)
       -612205764984*e1-3881941100694,e2],[e1^3+186*c3+31,e1],[c3^2+c3+1,c3],
  [c5^4+c5^3+c5^2+c5+1,c5]]]
  
Evaluation took 42.7050 seconds (48.6050 elapsed) using 25825.972 MB.

例３

(%i3) for i:1 thru 35 do (print([i]),p:x^i-2,RR7r_gp(cs_gap(spnGG_gp(p))))$
[1] 
Group(())
[2] 
Group([ (), (1,2) ])
[2,rem] 
[3] 
Group([ (), (2,3), (1,3,2), (1,2), (1,3), (1,2,3) ])
using a factor (-12*c3)+A^3-6 over the cyclotomic_3 
[3,rem] 
[4] 
Group([ (), (1,4), (2,3), (1,4)(2,3), (1,3)(2,4), (1,3,4,2), (1,2,4,3), (1,2)(3,4) ])
[2,rem] 
[2,rem] 
[2,rem] 
[5] 
<permutation group with 20 generators>
using a factor (-30*c5^3)+10*c5^2-20*c5+A^5-10 over the cyclotomic_5 
[5,rem] 
[6] 
Group([ (), (1,5)(2,6), (1,2)(3,4)(5,6), (1,6)(2,5)(3,4), (1,6)(2,4)(3,5), (1,2,4,6,5,3), (1,5,4)(2,3,6), (2,3)(4,5), (1,3,5,6,4,2), (1,3)(2,5)(4,6), (1,4)(3,6), (1,4,5)(2,6,3) ])
using a factor (-720*c3)+A^6-74 over the cyclotomic_3 
[2,rem] 
[3,rem] 
[7] 
<permutation group with 42 generators>
using a factor (-84*c7^5)-112*c7^4-28*c7^3-56*c7^2-140*c7+A^7-70 over the cyclotomic_21
  
[7,rem] 
[8] 
<permutation group with 16 generators>
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[9] 
<permutation group with 54 generators>
using a factor 1296*c3+A^18*((-1008*c3)-504)+A^27+17172*A^9+648 over the cyclotomic_3
  
[3,ls] 
[3,rem] 
[3,rem] 
[10] 
<permutation group with 40 generators>
using a factor (-26840*c5^3)-57200*c5^2-51480*c5+A^10-16282 over the cyclotomic_5
  
[2,rem] 
[5,rem] 
[11] 
<permutation group with 110 generators>
using a factor (-1254*c11^9)-220*c11^8-308*c11^7-990*c11^6+330*c11^5-352*c11^4-440*c11^3+594*c11^2-660*c11+A^11-330 over the cyclotomic_55
  
[11,rem] 
[12] 
<permutation group with 48 generators>
using a factor (-5100480*c3)+A^12*((-744480*c3)-18500)+A^24-21345404 over the cyclotomic_3
  
[2,rem] 
[2,rem] 
[2,rem] 
[3,rem] 
[13] 
<permutation group with 156 generators>
using a factor (-3146*c13^11)-2730*c13^10+858*c13^9-2600*c13^8-4004*c13^7-1144*c13^6-2548*c13^5-6006*c13^4-2418*c13^3-2002*c13^2-5148*c13+A^13-2574 over the cyclotomic_39
  
[13,rem] 
[14] 
<permutation group with 84 generators>
using a factor (-2996392*c7^5)-2076256*c7^4+590408*c7^3-1613920*c7^2-3503136*c7+A^14-613090 over the cyclotomic_21
  
[2,rem] 
[7,rem] 
[15] 
<permutation group with 120 generators>
using a factor ((-15780*c3)-26520)*c5^3+((-15780*c3)-3740)*c5^2-14480*c5-25092*c3+A^15-19786 over the cyclotomic_15
  
[3,rem] 
[5,rem] 
[16] 
<permutation group with 64 generators>
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[17] 
  *** nfisincl: Warning: increasing stack size to 16000000.
<permutation group with 272 generators>
using a factor (-51272*c17^15)-12104*c17^14-11016*c17^13-60996*c17^12-7616*c17^11-12342*c17^10-37128*c17^9+12376*c17^8-12410*c17^7-17136*c17^6+36244*c17^5-13736*c17^4-12648*c17^3+26520*c17^2-24752*c17+A^17-12376 over the cyclotomic_17
  
[17,rem] 
[18] 
<permutation group with 108 generators>
using a factor (-525994305879853440*c3)+A^36*((-609493248*c3)-5515782)+A^18*(349624993158156-362748920014656*c3)+A^54-143361159962807816 over the cyclotomic_3
  
[2,rem] 
[3,ls] 
[3,rem] 
[3,rem] 
[19] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfisincl: Warning: increasing stack size to 32000000.
<permutation group with 342 generators>
using a factor (-124032*c19^17)-101118*c19^16+83980*c19^15-102714*c19^14-108528*c19^13+50388*c19^12-100814*c19^11-155040*c19^10-46512*c19^9-100738*c19^8-251940*c19^7-93024*c19^6-98838*c19^5-285532*c19^4-100434*c19^3-77520*c19^2-201552*c19+A^19-100776 over the cyclotomic_57
  
[19,rem] 
[20] 
<permutation group with 160 generators>
using a factor 9284352000000*c5^3+A^20*((-1330401280*c5^3)+2469629120*c5^2-2134125600*c5+682330108)+23014398000000*c5^2+22270413000000*c5+A^40+7977616362500 over the cyclotomic_5
  
[2,rem] 
[2,rem] 
[2,rem] 
[5,rem] 
[21] 
  *** nfisincl: Warning: increasing stack size to 16000000.
<permutation group with 252 generators>
using a factor (677124*c3-619248)*c7^5+((-447300*c3)-1144066)*c7^4+((-447300*c3)-520072)*c7^3+(677124*c3+79534)*c7^2-1216838*c7-505398*c3+A^21-861118 over the cyclotomic_21
  
[3,rem] 
[7,rem] 
[22] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
<permutation group with 220 generators>
using a factor (-11229074560*c11^9)+6698642632*c11^8-2683141120*c11^7-5242592256*c11^6+9725452704*c11^5-6748408744*c11^4-1426168832*c11^3+5442664832*c11^2-11929283520*c11+A^22+1429976062 over the cyclotomic_55
  
[2,rem] 
[11,rem] 
[23] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfisincl: Warning: increasing stack size to 64000000.
  *** _*_: Warning: increasing stack size to 16000000.
<permutation group with 506 generators>
using a factor (-2124694*c23^21)-489808*c23^20-423016*c23^19-3194470*c23^18-472604*c23^17-486772*c23^16-2778446*c23^15-288420*c23^14-490268*c23^13-1470942*c23^12+490314*c23^11-490360*c23^10-692208*c23^9+1797818*c23^8-493856*c23^7-508024*c23^6+2213842*c23^5-557612*c23^4-490820*c23^3+1144066*c23^2-980628*c23+A^23-490314 over the cyclotomic_253
  
[23,rem] 
[24] 
<permutation group with 96 generators>
using a factor A^36*((-6432*c3)-3216)+A^12*((-32604864*c3)-16302432)+A^48-1797988*A^24+4 over the cyclotomic_3
  
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[3,rem] 
[25] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfisincl: Warning: increasing stack size to 64000000.
  *** _*_: Warning: increasing stack size to 16000000.
<permutation group with 500 generators>
using a factor A^50*(3628746377641385000*c5^3-1647791371390805000*c5^2+1980955006250580000*c5+990477503125290000)-188500000*c5^3+A^100*((-33218900*c5^3)+32156300*c5^2-1062600*c5-531300)+A^75*((-75134626573500*c5^3)-75134626573500*c5^2+115030173419500)+A^25*((-427357389517500000*c5^3)-427357389517500000*c5^2+269980735334750000)+44500000*c5^2-144000000*c5+A^125-72000000 over the cyclotomic_5
  
[5,ls] 
[5,rem] 
[5,rem] 
[26] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
<permutation group with 312 generators>
using a factor (-971321120640*c13^11)-254360271360*c13^10+414622391040*c13^9-591564945816*c13^8-397311582720*c13^7+543980124480*c13^6-352472480256*c13^5-757760340480*c13^4+231240186840*c13^3-242359104000*c13^2-1094179257600*c13+A^26-104832219650 over the cyclotomic_39
  
[2,rem] 
[13,rem] 
[27] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfisincl: Warning: increasing stack size to 64000000.
  *** _*_: Warning: increasing stack size to 16000000.
<permutation group with 486 generators>
using a factor A^54*(64185079264587155422066316743920384*c3+32092539632293577711033158371960192)+A^162*(646330905226424471479920*c3+323165452613212235739960)-1632586752*c3+A^216*((-168725700*c3)-84362850)+A^108*((-23162703161108643394416419869245312*c3)-11581351580554321697208209934622656)+A^243+26113852523044440*A^189+431757909098770766278078746432*A^135+515882115360428367277687574283383232*A^81+93715791643684117316945664*A^27-816293376 over the cyclotomic_3
  
[3,ls] 
[3,ls] 
[3,ls] 
[3,rem] 
[3,rem] 
[28] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
<permutation group with 336 generators>
using a factor 8310128683316942272*c7^5+A^28*((-14292346192992*c7^5)-7637767388160*c7^4+7443111224640*c7^3-6714427087872*c7^2-19353706444800*c7-3689457900548)-3955704597347134464*c7^4+9824604059141698176*c7^3-2664151871716256768*c7^2+6167144382212136960*c7+A^56+2799751623397086212 over the cyclotomic_21
  
[2,rem] 
[2,rem] 
[2,rem] 
[7,rem] 
[29] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfsplitting: Warning: increasing stack size to 64000000.
  *** nfisincl: Warning: increasing stack size to 128000000.
  *** subst: Warning: increasing stack size to 16000000.
  *** subst: Warning: increasing stack size to 32000000.
  *** _*_: Warning: increasing stack size to 64000000.
<permutation group with 812 generators>
  *** nffactor: Warning: increasing stack size to 16000000.
using a factor (-89224590*c29^27)-20029198*c29^26-16908450*c29^25-155757840*c29^24-19982508*c29^23-19792500*c29^22-175147530*c29^21-19079970*c29^20-20022702*c29^19-123821880*c29^18-11445720*c29^17-20029952*c29^16-60090030*c29^15+20030010*c29^14-20030068*c29^13-28614300*c29^12+83761860*c29^11-20037318*c29^10-20980050*c29^9+135087510*c29^8-20267520*c29^7-20077512*c29^6+115697820*c29^5-23151570*c29^4-20030822*c29^3+49164570*c29^2-40060020*c29+A^29-20030010 over the cyclotomic_203
  
[29,rem] 
[30] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
<permutation group with 240 generators>
using a factor ((-84445822933920*c3)-80494119004000)*c5^3+(9957570973280-34779365611320*c3)*c5^2+((-37324603531560*c3)-78290214838440)*c5-105867478586400*c3+A^30-37885424529826 over the cyclotomic_15
  
[2,rem] 
[3,rem] 
[5,rem] 
[31] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfsplitting: Warning: increasing stack size to 64000000.
  *** nfsplitting: Warning: increasing stack size to 128000000.
  *** nfisincl: Warning: increasing stack size to 256000000.
  *** subst: Warning: increasing stack size to 16000000.
  *** subst: Warning: increasing stack size to 32000000.
  *** _*_: Warning: increasing stack size to 64000000.
<permutation group with 930 generators>
  *** nffactor: Warning: increasing stack size to 16000000.
  *** nffactor: Warning: increasing stack size to 16000000.
  *** nffactor: Warning: increasing stack size to 16000000.
  *** nffactor: Warning: increasing stack size to 32000000.
  *** nffactor: Warning: increasing stack size to 64000000.
  *** nffactor: Warning: increasing stack size to 128000000.
  *** nffactor: Warning: increasing stack size to 256000000.
using a factor (-209664780*c31^29)-169345560*c31^28+243161520*c31^27-174603780*c31^26-169407560*c31^25+431735760*c31^24-169684452*c31^23-170817192*c31^22+361020420*c31^21-169353620*c31^20-185122080*c31^19+112896420*c31^18-169344692*c31^17-258048960*c31^16-80640300*c31^15-169344568*c31^14-451585680*c31^13-153567180*c31^12-169335640*c31^11-699709680*c31^10-167872068*c31^9-169004808*c31^8-770425020*c31^7-169281700*c31^6-164085480*c31^5-581850780*c31^4-169343700*c31^3-129024480*c31^2-338689260*c31+A^31-169344630 over the cyclotomic_465
  
[31,rem] 
[32] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
<permutation group with 256 generators>
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[2,rem] 
[33] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfsplitting: Warning: increasing stack size to 64000000.
  *** nfisincl: Warning: increasing stack size to 128000000.
  *** subst: Warning: increasing stack size to 16000000.
  *** _*_: Warning: increasing stack size to 32000000.
<permutation group with 660 generators>
using a factor c11^7*(519052776*c3+414162232)+c11^4*(519052776*c3-1195709680)-1920480816*c3+c11^2*(859393656-1137871680*c3)+c11^9*((-1137871680*c3)-3297865560)+c11^5*((-1331455950*c3)-513832374)+c11^6*((-1331455950*c3)-2118223800)+c11^8*((-3480414828*c3)-1221726616)+c11^3*((-3480414828*c3)-3559288436)-1300600224*c11+A^33-1610540520 over the cyclotomic_165
  
[3,rem] 
[11,rem] 
[34] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfsplitting: Warning: increasing stack size to 64000000.
  *** nfsplitting: Warning: increasing stack size to 128000000.
  *** subst: Warning: increasing stack size to 16000000.
  *** _*_: Warning: increasing stack size to 32000000.
<permutation group with 544 generators>
using a factor (-3808228426557440*c17^15)-7919863789291520*c17^14-3403121175472128*c17^13+1279988834931712*c17^12-3539846083028992*c17^11-8119861978524672*c17^10-3604322525292544*c17^9+372311085462272*c17^8-3225651920873472*c17^7-6439119406838272*c17^6-4240802890164224*c17^5-1573811911309704*c17^4-2076123785922560*c17^3-4675445439768440*c17^2-5956765649455104*c17+A^34-2908228400359426 over the cyclotomic_17
  
[2,rem] 
[17,rem] 
[35] 
  *** nfsplitting: Warning: increasing stack size to 16000000.
  *** nfsplitting: Warning: increasing stack size to 32000000.
  *** nfsplitting: Warning: increasing stack size to 64000000.
  *** nfsplitting: Warning: increasing stack size to 128000000.
  *** subst: Warning: increasing stack size to 16000000.
  *** subst: Warning: increasing stack size to 32000000.
  *** _*_: Warning: increasing stack size to 64000000.
<permutation group with 840 generators>
using a factor ((-2814705810*c5^3)-11072532380*c5^2-1236699170*c5-9449209994)*c7^5+((-12865509020*c5^3)-12027706250*c5^2-11980726170*c5-18890856012)*c7^4+((-2956013550*c5^3)-2118210780*c5^2-11980726170*c5-9081390038)*c7^3+(6832839580*c5^3-1424986990*c5^2-1236699170*c5-7779009056)*c7^2+((-3002993630*c5^3)-3002993630*c5^2-15991519880)*c7-7609289760*c5^3+1673794090*c5^2-2932502040*c5+A^35-9462010960 over the cyclotomic_105
  
[5,rem] 
[7,rem] 
Evaluation took 467.7820 seconds (6274.2230 elapsed) using 340797.419 MB.

2019-04-05

位数が大きな場合

これまでの RR シリーズでは，分解体の定義多項式，primitive element による入力多項式の根の表示， primitive element を根の $\mathbb{Z}$ 線型結合で表した際の係数を古典的な Trager の方法（ http://www.cecm.sfu.ca/personal/monaganm/teaching/TopicsinCA17/TragerFactor.pdf ）により（ http://ehito.hatenablog.com/entry/2019/02/24/150254 ），また，組成列も共役類の組み合わせ（ http://ehito.hatenablog.com/entry/2019/02/13/200937 ）から得ていましたが，今回は，galois 群の位数が数百程度の場合にも対応できるよう，外部ツールを用いるスタイルで再び実装しました．ただし，分解体と冪根の中間体上の定義多項式を同時に得るためにかつて用いた Groebner 基底（ by asir ）による方法は，次数や変数の個数の増大に敏感なため採用せず，同じく，代数体上の因数分解や GCD の利用も最小限に留めています．

具体的には
・分解体の $\mathbb{Q}$ 上の定義多項式には，pari の nfsplitting （LLL アルゴリズムによるもの）
・分解体の primitive element による入力多項式の根の表示には，同じく pari の nfisincl
・galois 群（置換表現および同型写像表現）の生成には，独自アルゴリズム（多倍長浮動小数点数によるもの）
・組成列の生成には，gap の MaximalNormalSubgroups
・円分体およびその部分体上の因数分解には，pari の nfsubfields，nffactor
・分解体の各中間体上の定義多項式には，分解体の primitive element による添加する冪根の表示（１次のみ）を用いた簡約，そのフォールバックとして Lagrange Resolvents の総和
・各中間体上の加減乗除算，GCD 計算には，maxima の algebraic モード，gcd:subres
をそれぞれ利用しています．

以下，取り敢えず，実行データを掲載します．リストの要素は
・サンプル番号
・入力多項式
・galois 群の位数
・各中間体間の拡大次数
・分解体の $\mathbb{Q}$ 上の定義多項式，primitive element による入力多項式の根の表示から，galois 群さらに組成列の生成までの時間（秒）
・分解体の各中間体上の定義多項式の生成から冪根による primitive element の表示までの時間（秒）
・上記２つの時間の合計（秒）
です．

【サンプルセット１】
サンプル番号 16 以降は，先行研究
https://core.ac.uk/download/pdf/81182361.pdf
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0920-2.pdf
http://www.jssac.org/Editor/Suushiki/V09/No1/V9N1_108.pdf
http://www.icm.tu-bs.de/ag_algebra/software/distler/Diplom.pdf （RadiRoot https://gap-packages.github.io/radiroot/ の作者の学位論文）

などからのものです．

       [[1,x^2-2,[2],[2],0.708,0.002,0.71],
       [2,x^3-3*x-1,[3],[3],0.552,0.139,0.691],
       [3,x^4-2,[8],[2,2,2],0.37,0.006,0.376],
       [4,x^4+x^2-1,[8],[2,2,2],0.509,0.006,0.515],
       [5,x^4-2*x^3+2*x^2+2,[12],[3,2,2],0.842,0.134,0.976],
       [6,x^4+2*x^3+3*x^2+4*x+5,[24],[2,3,2,2],0.454,0.585,1.04],
       [7,x^4+x+1,[24],[2,3,2,2],0.376,0.829,1.21],
       [8,x^5-2,[20],[2,2,5],1.78,0.387,2.16],
       [9,x^5-5*x+12,[10],[2,5],0.455,0.302,0.757],
       [10,x^5+20*x+32,[10],[2,5],0.941,0.756,1.7],
       [11,x^5+11*x+44,[10],[2,5],0.161,0.404,0.565],
       [12,x^5+x^4-4*x^3-3*x^2+3*x+1,[5],[5],0.277,0.178,0.455],
       [13,x^5+100*x^2+1000,[20],[2,2,5],0.845,0.285,1.13],
       [14,x^6+x^3+1,[6],[2,3],0.519,0.15,0.669],
       [15,x^6-2,[12],[2,2,3],0.396,0.571,0.967],
       [16,x^5-5*x^3+5*x-5,[20],[2,2,5],0.245,0.433,0.678],
       [17,x^6+x^3+7,[18],[2,3,3],0.35,0.106,0.456],
       [18,x^6-3*x^4+1,[24],[2,3,2,2],0.894,0.32,1.21],
       [19,x^6+x^4-9,[24],[2,3,2,2],0.171,0.625,0.796],
       [20,x^6+x^4-8,[48],[2,2,3,2,2],0.734,1.45,2.19],
       [21,x^6+x^4-x^2+5*x-5,[72],[2,2,2,3,3],4.27,34.8,39.1],
       [22,x^7+7*x^3+7*x^2+7*x-1,[14],[2,7],0.163,0.456,0.619],
       [23,x^7-14*x^5+56*x^3-56*x+22,[21],[3,7],0.202,1.34,1.54],
       [24,x^7-2,[42],[2,3,7],0.56,1.29,1.85],
       [25,x^8-2*x^6-x^4+7*x^2-5*x+1,[16],[2,2,2,2],0.479,0.043,0.522],
       [26,x^9+x^8+3*x^6+3*x^3-3*x^2+5*x-1,[18],[2,3,3],0.337,0.321,0.658],
       [27,x^12-3,[24],[2,2,2,3],0.659,0.109,0.768],
       [28,x^7-14*x^5+56*x^3-56*x+22,[21],[3,7],0.538,0.475,1.01],
       [29,
        x^15-x^14-14*x^13+13*x^12+78*x^11-66*x^10-220*x^9+165*x^8+330*x^7
            -210*x^6-252*x^5+126*x^4+84*x^3-28*x^2-8*x+1,[15],[3,5],1.25,
        0.321,1.57]]
       [30,
        x^14+28*x^11+28*x^10-28*x^9+140*x^8+360*x^7+147*x^6+196*x^5+336*x^4
            -546*x^3-532*x^2+896*x+823,[98],[2,7,7],7.114,199.4,206.5]]

サンプル番号 30 の冪根表示．

[[c7^2*(2*e3^4-e3^2+e2^6+e2^3)+c7^3*(2*e3^4+e2^5)+c7*(e3^4-e3^2+3*e2^6+e2^3)
                               +c7^4*(e3^4+3*e2^6+e2^3)+e3
                               +c7^5*(3*e2^6-e2^5+e2^3)+e2^6+e2^5+A,A],
  [e3^7+2*c7^5-c7^4+2*c7^3-c7^2+2*c7,e3],
  [e2^7-4*c7^5-c7^4-3*c7^3-3*c7^2-c7-4,e2],
  [c7^6+c7^5+c7^4+c7^3+c7^2+c7+1,c7]]

【サンプルセット２】
$x^n-2\ (n=1,\ldots,30)$ （一部サンプルセット１と重複）．一般の場合の位数は，https://mathoverflow.net/questions/143739/galois-group-of-xn-2 にあります．

      [[1,x-2,[1],[],1.193,0.0,1.193],
       [2,x^2-2,[2],[2],1.147,0.001,1.148],
       [3,x^3-2,[6],[2,3],1.172,0.09,1.262],
       [4,x^4-2,[8],[2,2,2],1.202,0.012,1.214],
       [5,x^5-2,[20],[2,2,5],1.153,0.186,1.339],
       [6,x^6-2,[12],[2,2,3],1.232,0.185,1.417],
       [7,x^7-2,[42],[2,3,7],1.314,0.526,1.84],
       [8,x^8-2,[16],[2,2,2,2],1.252,0.015,1.267],
       [9,x^9-2,[54],[2,3,3,3],1.295,0.21,1.505],
       [10,x^10-2,[40],[2,2,2,5],1.435,3.87,5.305],
       [11,x^11-2,[110],[2,5,11],1.837,0.926,2.763],
       [12,x^12-2,[48],[2,2,2,2,3],1.748,0.281,2.029],
       [13,x^13-2,[156],[2,2,3,13],4.897,1.238,6.135],
       [14,x^14-2,[84],[2,2,3,7],2.074,0.665,2.739],
       [15,x^15-2,[120],[2,2,2,3,5],2.333,1.345,3.678],
       [16,x^16-2,[64],[2,2,2,2,2,2],1.824,0.147,1.971],
       [17,x^17-2,[272],[2,2,2,2,17],13.31,4.305,17.62],
       [18,x^18-2,[108],[2,2,3,3,3],3.449,0.752,4.201],
       [19,x^19-2,[342],[2,3,3,19],18.02,10.46,28.49],
       [20,x^20-2,[160],[2,2,2,2,2,5],7.155,2.767,9.922],
       [21,x^21-2,[252],[2,2,3,3,7],11.41,3.08,14.49],
       [22,x^22-2,[220],[2,2,5,11],15.8,3.614,19.41],
       [23,x^23-2,[506],[2,11,23],58.19,53.77,112.0],
       [24,x^24-2,[96],[2,2,2,2,2,3],2.518,0.941,3.459],
       [25,x^25-2,[500],[2,2,5,5,5],71.24,49.02,120.3],
       [26,x^26-2,[312],[2,2,2,3,13],55.11,8.613,63.72],
       [27,x^27-2,[486],[2,3,3,3,3,3],77.09,53.58,130.7],
       [28,x^28-2,[336],[2,2,2,2,3,7],80.96,19.26,100.2],
       [29,x^29-2,[812],[2,2,7,29],360.1,169.8,529.9],
       [30,x^30-2,[240],[2,2,2,2,3,5],16.68,4.233,20.91]]
Evaluation took 352.3320 seconds (1212.0310 elapsed) using 229011.373 MB.

サンプル番号 29 の冪根表示．

[[e4+A,A],
  [e4^29+89224590*c29^27+20029198*c29^26+16908450*c29^25+155757840*c29^24
        +19982508*c29^23+19792500*c29^22+175147530*c29^21+19079970*c29^20
        +20022702*c29^19+123821880*c29^18+11445720*c29^17+20029952*c29^16
        +60090030*c29^15-20030010*c29^14+20030068*c29^13+28614300*c29^12
        -83761860*c29^11+20037318*c29^10+20980050*c29^9-135087510*c29^8
        +20267520*c29^7+20077512*c29^6-115697820*c29^5+23151570*c29^4
        +20030822*c29^3-49164570*c29^2+40060020*c29+20030010,e4],
  [c29^28+c29^27+c29^26+c29^25+c29^24+c29^23+c29^22+c29^21+c29^20+c29^19
         +c29^18+c29^17+c29^16+c29^15+c29^14+c29^13+c29^12+c29^11+c29^10+c29^9
         +c29^8+c29^7+c29^6+c29^5+c29^4+c29^3+c29^2+c29+1,c29]]

2019-03-20

QE による検証

Mathematica の QE のデフォルトの議論領域は

Reduce[Exists[x, a*x^2 == 1]]

に対する出力

からも判るように複素数体であり，前回公開した Mathematica での実装の目的の 1 つは，この QE による結果の検証でした．

Mathematica で前回の各関数の定義コードを実行した後，例えば，

(p1=PL[[1]])@x

を

mp[p1];nGG[];cs[];RR[];InputForm@DP

のように処理すると

といった出力が得られます．

このとき，A についての 2 つの条件
(1) A が分解体の primitive element の定義多項式 p2 の零となる
(2) A の多項式で表された根全体 r1 /. pe -> A が入力の多項式 p1 の根全体となる
が等価であるという式

ForAll[A, 
 Equivalent[p2@A == 0, 
  ForAll[x, Times @@ (x - r1 /. pe -> A) == p1@x]]]

すなわち

を複素数体上で

Reduce[%,Complexes]

のように QE すると

と答えてくれます．

また，A についての 2 つの条件
(1) A が分解体の primitive element の定義多項式 p2 の零となる
(3) 出力 DP に属する全ての多項式の共通の零点 (w,e[1]) が存在する
が等価であるという式

ForAll[A, 
 Equivalent[p2@A == 0, 
  Exists[Evaluate@Rest@vs, And @@ (# == 0 & /@ DP)]]]

すなわち

を複素数体上で

Reduce[%,Complexes]

のように QE すると

と答えてくれます．

2019-03-16

Mathematica 推参

オリジナルプログラムの元になったコードは Mathematica で書かれていますが，汎用性を重視した筆致なので，今回は
https://reference.wolfram.com/language/tutorial/AlgebraicNumberFields.html.ja
にある代数体関連の組み込み関数などを用いて書いてみました（取り敢えず動く程度）．

なお，https://develop.open.wolframcloud.com/app/ の Create a New Notebook ボタンを押すと Mathematica がオンラインで利用できます．

(* mp *)
mp[p1_]:=Block[{c,x},
n1=Range@Exponent[p1@x,x];
r1=ToNumberField[AlgebraicNumber[Root[p1,#],{0,1}]&/@n1,All];
p2=(pe=r1[[1,1]])[[1]];(* pe is not a "AlgebraicNumber" *)
c1=Map[c,n1];
c1=c1/.SolveAlways[x==r1.c1/.pe->x,x][[1]]/.c[_]->0];

(* nGG *)
nGG[]:=Block[{x},
r12=Map[ToString,Chop[N[r1/.pe->x/.NSolve[p2@x,WorkingPrecision->50],10]],{2}];
gg=PermutationCycles/@(r12/.Thread[r12[[pe[[2]]]]->n1]);
r2=r1.Permute[c1,#]&/@gg];

(* csc and cs *)
csc[gg0_]:=Block[{},
cc=Rest@GroupOrbits[PermutationGroup@gg0,gg0];
Last@SortBy[Select[Append[#,Cycles[{}]]&/@(Union@@#&/@Subsets@cc),2*Length@#<=Length@gg0&&
GroupOrder@PermutationGroup@#==Length@#&],Length]];
cs[]:=Block[{},
cs1=NestWhileList[csc,gg,Length@#>1&];
cs2=Length/@cs1;cs3=Table[cs2[[i]]/cs2[[i+1]],{i,Length@cs2-1}]];

(* RR *)
Off[ToNumberField::nalg];
RR[]:=Block[{},
w1=ToNumberField@Exp[2*Pi*I/(ppp=LCM@@cs3)];
Print["using Cyclotomic_",ppp];
DP={Cyclotomic[ppp,w],
If[ppp==2,p2@A,First@Last@FactorList[p2@A,Extension->w1]/.p_AlgebraicNumber->ToNumberField[p,w1]/.w1[[1]]->w]};
For[i=1,i<Length@cs2,i++,LRx=Sum[w^Mod[ppp/pp*j,ppp]*Product[x-r2[[Position[gg,s][[1,1]]]],{s,PermutationProduct[PermutationPower[Complement[cs1[[i]],cs1[[i+1]]][[1]],j],#]&/@cs1[[i+1]]}],{j,pp=cs3[[i]]}];
ai=0;j=1;While[ai==0,ai=Simplify[LRx/.{w->w^j,pe->A},And@#==0&/@DP];j++];
DP=GroebnerBasis[Append[DP,Last@CoefficientList[ai,x]-e[i]],vs=Join[{A},Map[e,Reverse@Range@i],{w}]];(*Print@nputForm@DP*)]];

実行例．例によって，入力多項式の根の表示は長いので略します．

(* expamles *)
PL={#^3-3*#-1&,#^4-2&,#^4+#^2-1&,#^4-2*#^3+2*#^2+2&,#^4+2*#^3+3*#^2+4*#+5&,#^4+#+1&,#^5-2&,#^5-5*#+12&,#^5+20*#+32&,#^5+11*#+44&,#^5+#^4-4*#^3-3*#^2+3*#+1&,#^5+100*#^2+1000&,#^6+#^3+1&,#^6-2&};
(mp[#];nGG[];cs[];RR[];Print@InputForm@DP)&/@PL;//Timing